¿Qué es el Cálculo Diferencial e Integral?

El cálculo diferencial e integral es una rama de las matemáticas que se desarrolló progresivamente a través de la historia, con raíces en la Antigua Grecia y contribuciones de civilizaciones árabes e hindúes, hasta su florecimiento durante el Renacimiento.

Su desarrollo histórico puede dividirse en tres grandes períodos:

1. Anticipación (hasta 1600): Donde figuras como Cavalieri y Descartes sentaron las bases.
2. Desarrollo (1700): Newton y Leibniz unificaron técnicas previas bajo los conceptos de derivada e integral.
3. Formalización (1800): Matemáticos como Cauchy y Riemann reformularon estos conceptos en términos de límites.

El cálculo ha sido fundamental para explicar fenómenos en física, ingeniería, astronomía e incluso en ciencias biológicas y químicas. Su aplicación en estas últimas áreas puede ser directa o a través de la física, permitiendo el estudio de procesos como la circulación sanguínea, reacciones químicas o dinámica poblacional.

📌 Importante: La conexión más profunda entre las matemáticas y las ciencias naturales se establece mediante los modelos matemáticos, especialmente aquellos basados en el cálculo diferencial e integral, que nos permiten estudiar cómo cambian los sistemas a lo largo del tiempo.

Modelos Matemáticos: Nuestra Ventana a la Realidad

Un modelo matemático es una representación simplificada de un sistema real, utilizando el lenguaje y las herramientas matemáticas para capturar sus aspectos esenciales.

Características de los modelos matemáticos:

• No existe un único modelo para un sistema real: Podemos crear múltiples modelos según nuestro enfoque e interés.
• Simplificación: Reducimos un sistema complejo a sus variables más relevantes.
• Uso del lenguaje matemático: Expresamos las relaciones mediante ecuaciones y funciones.
• Retroalimentación: Las predicciones del modelo se contrastan con datos experimentales para validarlo.

El ciclo de modelado matemático incluye:

1. Formular hipótesis sobre el sistema
2. Expresarlas matemáticamente
3. Deducir consecuencias
4. Contrastarlas con la realidad
5. Ajustar o reformular el modelo si es necesario

En el cálculo infinitesimal, los modelos se enfocan principalmente en el estudio del cambio, utilizando funciones como herramienta fundamental para relacionar cantidades numéricas.

Tipos de modelos:

• Modelos deterministas: Establecen relaciones de causa-efecto precisas entre variables.
• Modelos empíricos o estadísticos: Se construyen a partir de datos experimentales, sin necesariamente explicar las causas subyacentes.

📌 Nota importante: Los modelos estadísticos no pretenden establecer relaciones causales, sino describir patrones en los datos de manera que capten las características principales del sistema.

Modelos Lineales: La Base del Análisis Matemático

Un modelo lineal es una representación matemática donde una variable dependiente se relaciona con una variable independiente mediante una ecuación lineal de la forma:

Ecuaciones lineales y rectas

Una recta en el plano (no vertical) se describe mediante la ecuación:

$$y = mx + b$$

Donde:

• m es la pendiente que determina la inclinación de la recta
• b es la ordenada al origen, el punto donde la recta interseca el eje y

La pendiente se calcula como: $$m = \frac{\text{variación vertical}}{\text{variación horizontal}} = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1}$$

Rectas paralelas y perpendiculares

Rectas paralelas: Dos rectas no verticales son paralelas si y solo si tienen la misma pendiente.

Rectas perpendiculares: Dos rectas (ninguna vertical) con pendientes m₁ y m₂ son perpendiculares si y solo si m₁m₂ = -1.

Por ejemplo, si una recta tiene pendiente m = -3, cualquier recta con pendiente m = 1/3 será perpendicular a ella.

📌 Para recordar: Las rectas horizontales (pendiente 0) son perpendiculares a las rectas verticales (que no tienen pendiente definida).

Modelos Lineales Deterministas

En la vida cotidiana usamos constantemente modelos lineales, especialmente para conversiones de unidades. Por ejemplo, la conversión entre temperaturas en grados Celsius y Fahrenheit sigue el modelo lineal:

$$$°F$ = \frac{9}{5}$°C$ + 32$$

Esta ecuación nos permite convertir cualquier temperatura entre estos sistemas de manera precisa. Si graficamos esta relación, obtendremos una recta donde:

• El eje x representa los grados Celsius
• El eje y representa los grados Fahrenheit
• La pendiente es 9/5
• La ordenada al origen es 32

Otro ejemplo útil es la presión del aire para un buzo. Esta presión varía linealmente con la profundidad. Si a 10 metros la presión es 2.02 atmósferas y a 20 metros es 3.04 atmósferas, podemos determinar la presión a cualquier profundidad usando el modelo lineal:

$$P = 1 + 0.102 \times \text{profundidad}$$

Donde la profundidad se mide en metros y P en atmósferas. Esto significa que:

• En la superficie (0 metros): P = 1 atmósfera
• A 15 metros: P = 2.53 atmósferas
• A 40 metros: P = 5.08 atmósferas

📌 Aplicación práctica: Los modelos lineales son fundamentales para comprender relaciones proporcionales en ciencias exactas y naturales, permitiéndonos hacer predicciones precisas.

Modelos Lineales Estadísticos

En la naturaleza, no todas las relaciones son perfectamente lineales. Sin embargo, el modelo lineal sigue siendo útil para aproximar relaciones complejas utilizando datos experimentales.

Consideremos un estudio sobre el peso al nacer y las semanas de gestación de 32 bebés. Los datos se presentan dispersos, pero podemos crear un modelo lineal que los aproxime mediante la ecuación:

$$p = m \cdot s + b$$

Donde:

• p: peso del bebé al nacer (en kg)
• s: semanas de gestación
• m: pendiente (tasa de cambio del peso por semana)
• b: ordenada al origen

Error Cuadrático Medio (ECM)

Para determinar qué modelo lineal se ajusta mejor a los datos, utilizamos el concepto de residuo y error cuadrático medio:

• Residuo: Diferencia vertical entre un valor observado y el valor correspondiente en la recta del modelo
• ECM: Promedio de los residuos elevados al cuadrado

$$\text{ECM} = \frac{\sum_{i=1}^{n} $y_i - \hat{y}_i$^2}{n}$$

Donde:

• y_i: valor observado
• \hat{y}_i: valor predicho por el modelo

El ECM nos ayuda a identificar cuantitativamente cuál modelo se ajusta mejor a los datos:

• Siempre es ≥ 0
• Solo es igual a 0 cuando la recta pasa exactamente por todos los puntos
• Un valor cercano a 0 indica un buen ajuste

📌 Concepto clave: El modelo con el menor ECM es matemáticamente el que mejor representa la relación entre las variables, aunque siempre debemos considerar el contexto biológico o físico.

Método de Mínimos Cuadrados

El método de mínimos cuadrados nos permite encontrar la recta que minimiza el Error Cuadrático Medio, proporcionando así el mejor ajuste lineal posible a un conjunto de datos.

Procedimiento con herramientas digitales:

Utilizando software como Desmos, podemos:

1. Ingresar los datos en una tabla
2. Indicar que queremos un ajuste lineal usando la notación y ~ mx + b
3. El software calcula automáticamente los valores óptimos de m y b

Para nuestro ejemplo de peso de bebés y semanas de gestación, el mejor modelo es:

$$p = 0.131093s - 2.04726$$

Esto significa que:

• Por cada semana adicional de gestación, el peso aumenta aproximadamente 0.131 kg
• La ordenada al origen $-2.04726 kg$ no tiene interpretación física directa en este contexto

Aplicación práctica: Chirridos de grillos

Existe una relación entre la temperatura ambiente y la cantidad de chirridos que emiten los grillos. Un método casero dice que:

$$\text{Temperatura (°C)} = \frac{\text{Chirridos por minuto}}{7} + 4$$

Al aplicar mínimos cuadrados a datos experimentales, encontramos una relación ligeramente diferente. Este ejemplo ilustra cómo los modelos lineales pueden utilizarse para:

• Cuantificar relaciones naturales
• Crear "termómetros biológicos"
• Predecir variables basadas en observaciones indirectas

📌 Limitaciones importantes: El modelo solo es válido en el rango de temperaturas estudiado (aproximadamente 11°C a 27°C) y no explica la causalidad entre las variables.

Introducción a las Funciones Numéricas

Las funciones son herramientas matemáticas fundamentales para modelar relaciones entre cantidades. Una función numérica es una regla que asigna a cada elemento de un conjunto numérico exactamente un elemento de otro conjunto numérico.

Elementos fundamentales de una función:

$$f: A \rightarrow B$$

Donde:

• f es el nombre de la función
• A es el dominio (conjunto de entrada)
• B es el codominio (conjunto de salida)
• x es la variable independiente
• y = f(x) es la variable dependiente

Cuando escribimos y = f(x), decimos que:

• y es f evaluada en x
• y es f de x
• y es la imagen de x mediante la función f

⚠️ Atención: Los paréntesis en f(x) no indican multiplicación, sino la aplicación de la función f al valor x.

Dominio natural de una función

El dominio está determinado por:

1. Motivos relacionados con el contexto:

   • Si f representa longitud, área o volumen, no puede ser negativa
   • Si P representa una población, debe ser un número natural
   • Restricciones físicas como temperaturas mínimas posibles

2. Limitaciones matemáticas:

   • No se permite dividir por cero
   • No se pueden calcular raíces cuadradas de números negativos

3. Motivos arbitrarios que decide cada persona según el contexto del problema

El dominio natural es el mayor conjunto de números reales para los cuales la función está definida matemáticamente.

Imagen y Gráfica de una Función Numérica

Imagen de una función

La imagen de una función f es el conjunto de todos los valores que efectivamente alcanza la función:

$$\text{Im}(f) = {f(x): x \in A}$$

Es decir, son todos los valores de salida que la función produce para su dominio. Por ejemplo:

• Para f(x) = x², Im(f) = [0,+∞) porque los resultados siempre son no negativos
• Para f(x) = √x, Im(f) = [0,+∞)

📌 Nota: Calcular la imagen de una función no siempre es sencillo, especialmente para funciones complejas.

Gráfica de una función numérica

La gráfica de una función f está formada por todos los puntos (x, y) del plano tales que y = f(x) para x ∈ Dom(f). Estos puntos representan pares de entrada-salida de la función.

La gráfica nos permite visualizar:

• El dominio (proyectado sobre el eje x)
• La imagen (proyectado sobre el eje y)
• El comportamiento general de la función

Prueba de la recta vertical

Una curva en el plano xy es la gráfica de una función de x si y solo si ninguna recta vertical interseca la curva más de una vez.

Esto es consecuencia directa de la definición de función: a cada valor de x le corresponde exactamente un valor de y. Si una recta vertical x = a interseca la curva más de una vez, entonces existirían múltiples valores de y para un mismo x, lo que violaría la definición de función.

Por ejemplo, la curva x = y² - 2 no es la gráfica de una función de x porque hay rectas verticales que la cortan dos veces. Sin embargo, contiene las gráficas de dos funciones: f(x) = +√$x+2$ y g(x) = -√$x+2$.

Funciones Definidas por Partes

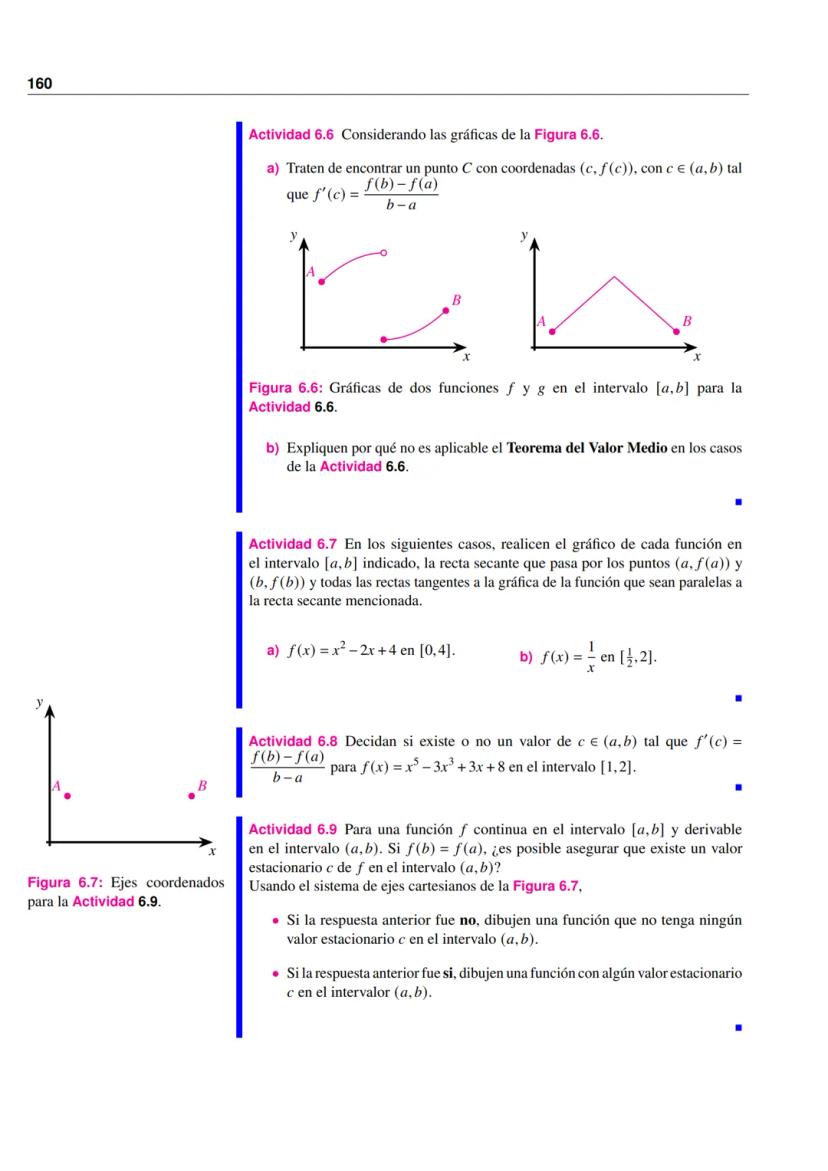
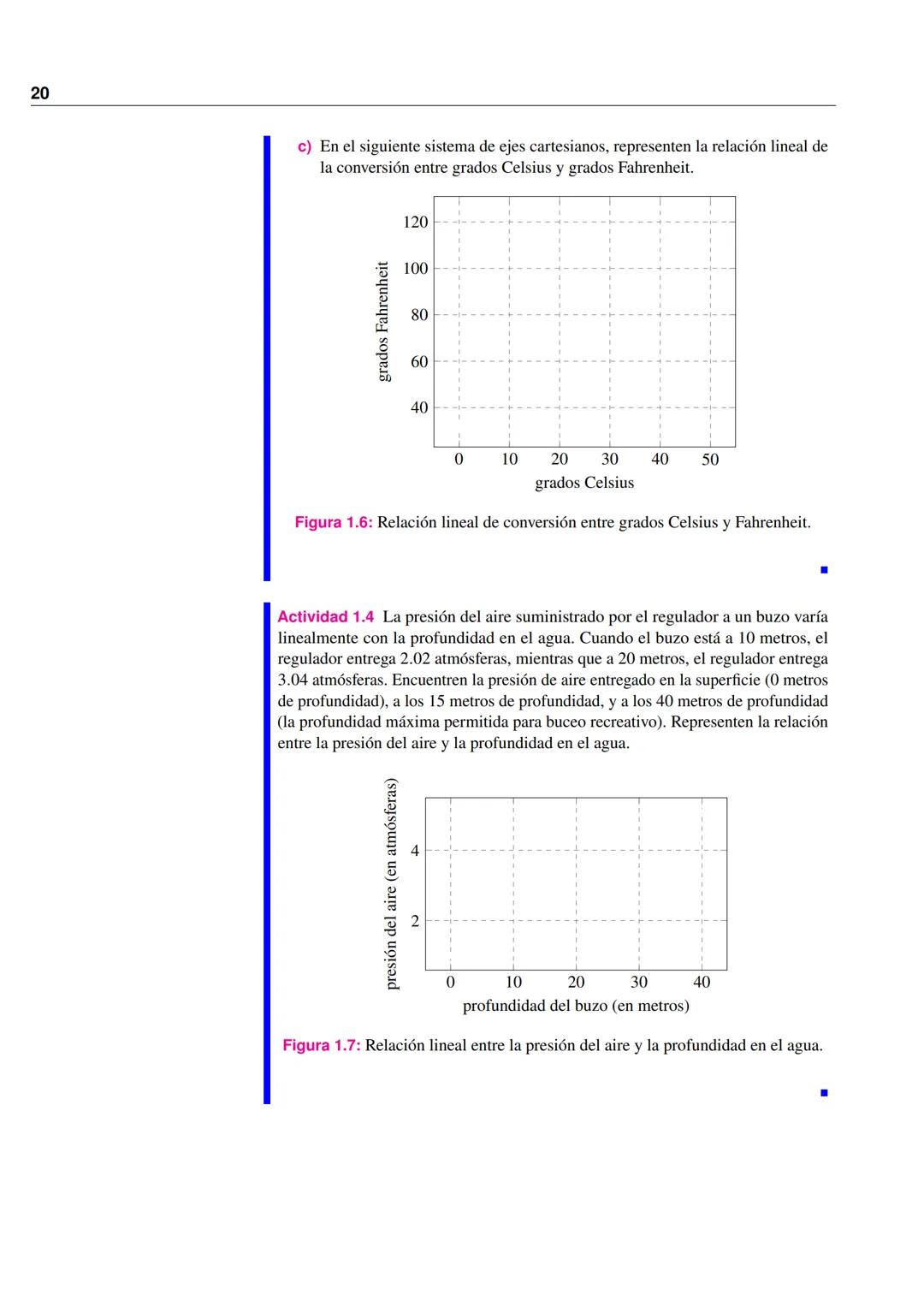
En muchas situaciones prácticas, una función puede comportarse de diferentes maneras según el valor de la variable independiente. Estas se llaman funciones definidas por partes.

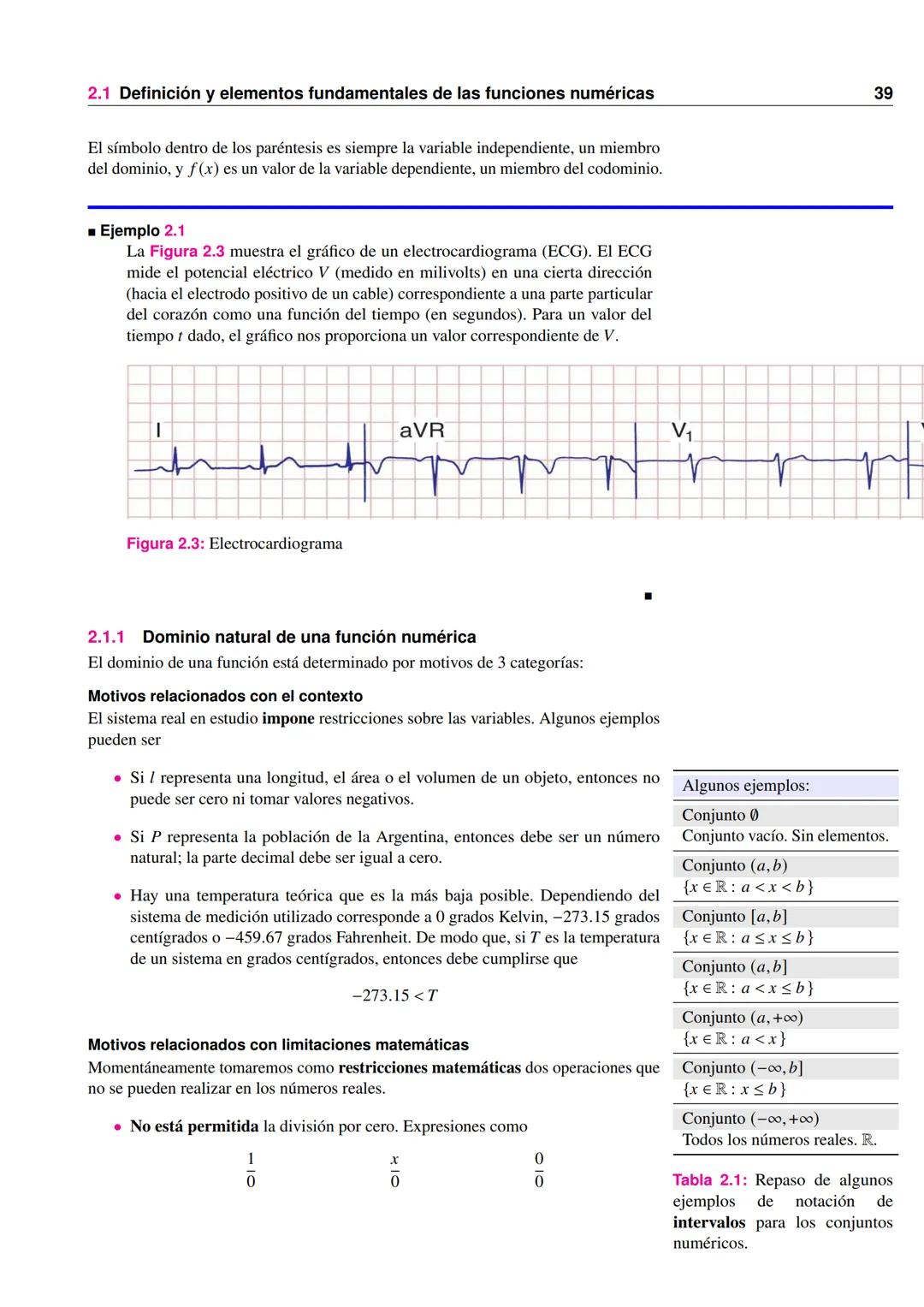
Ejemplo práctico: Dosificación de medicamentos

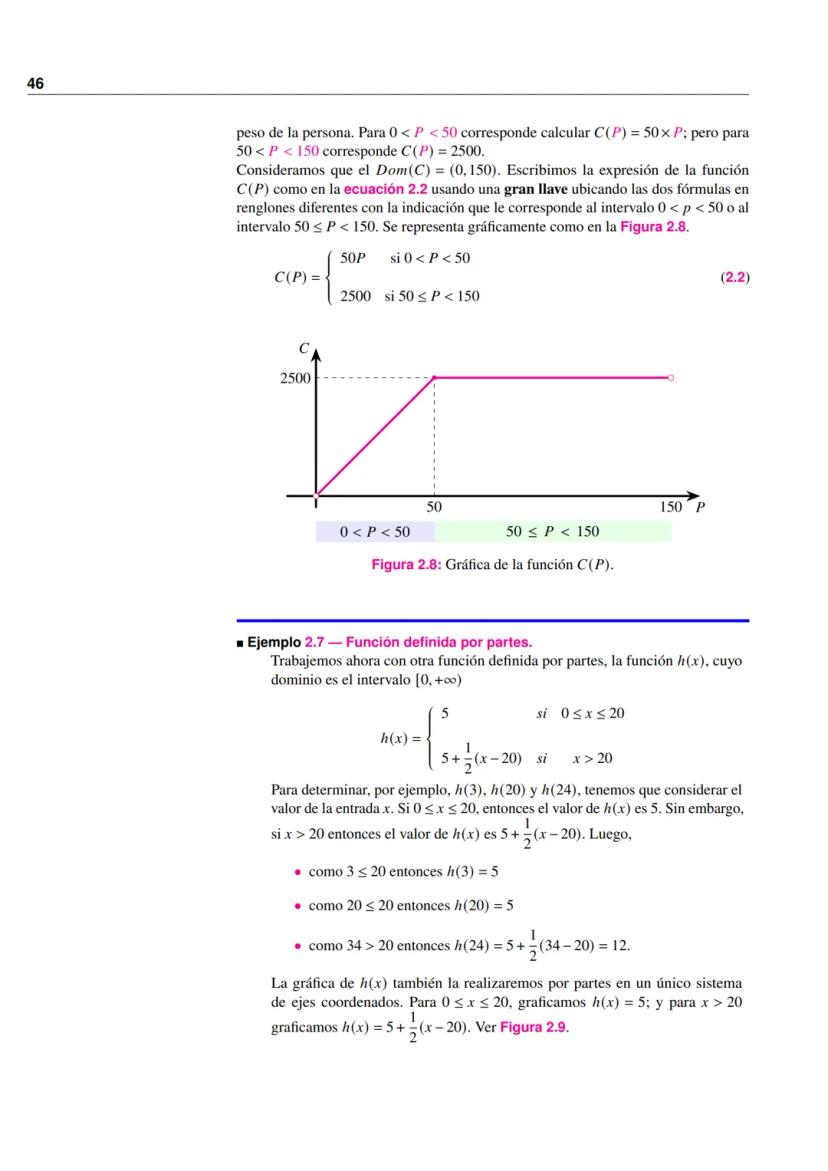
Un medicamento tiene una dosis de 10 mg/kg por toma, con máximo 5 tomas diarias, sin sobrepasar 2500 mg al día. Para pacientes con peso P (en kg), la dosis máxima diaria es:

$$C(P) = \begin{cases} 50P & \text{si } 0 < P < 50 \ 2500 & \text{si } 50 \leq P < 150 \end{cases}$$

Esta función tiene dos comportamientos:

• Para pesos menores a 50 kg: la dosis aumenta proporcionalmente con el peso
• Para pesos entre 50 y 150 kg: la dosis se mantiene constante en 2500 mg

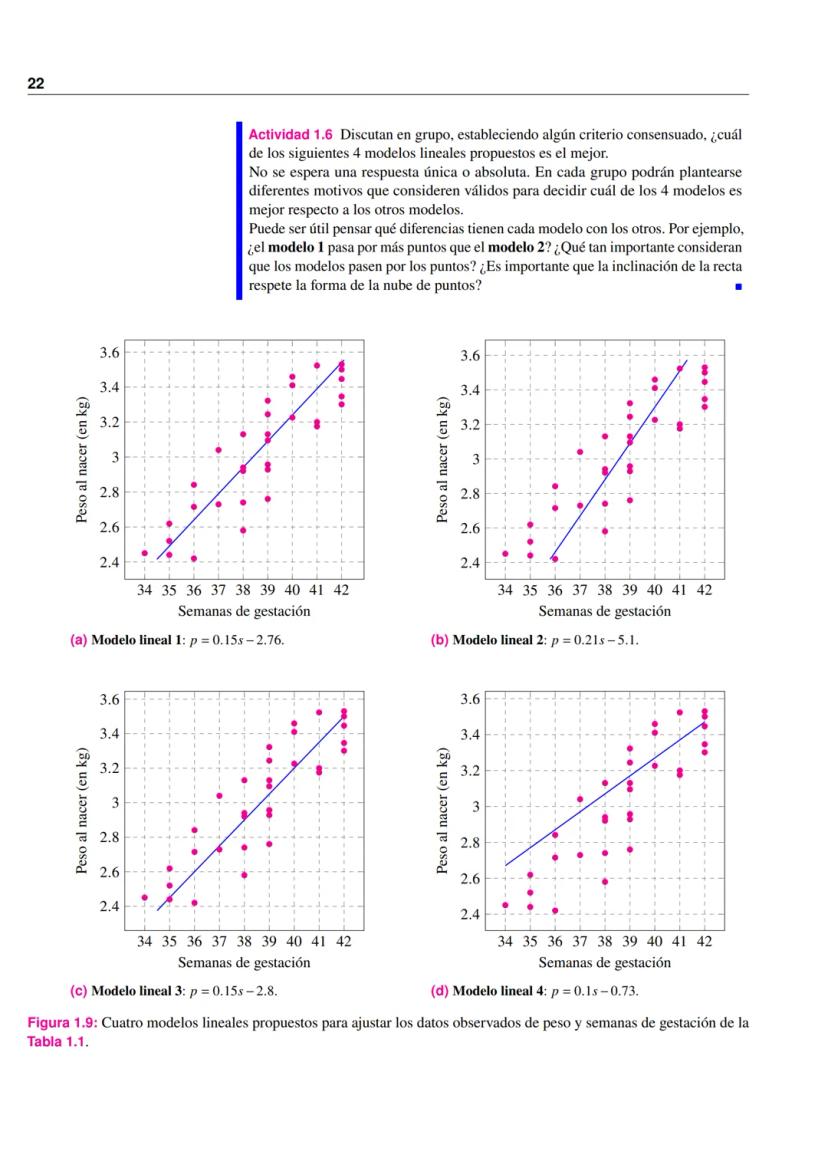
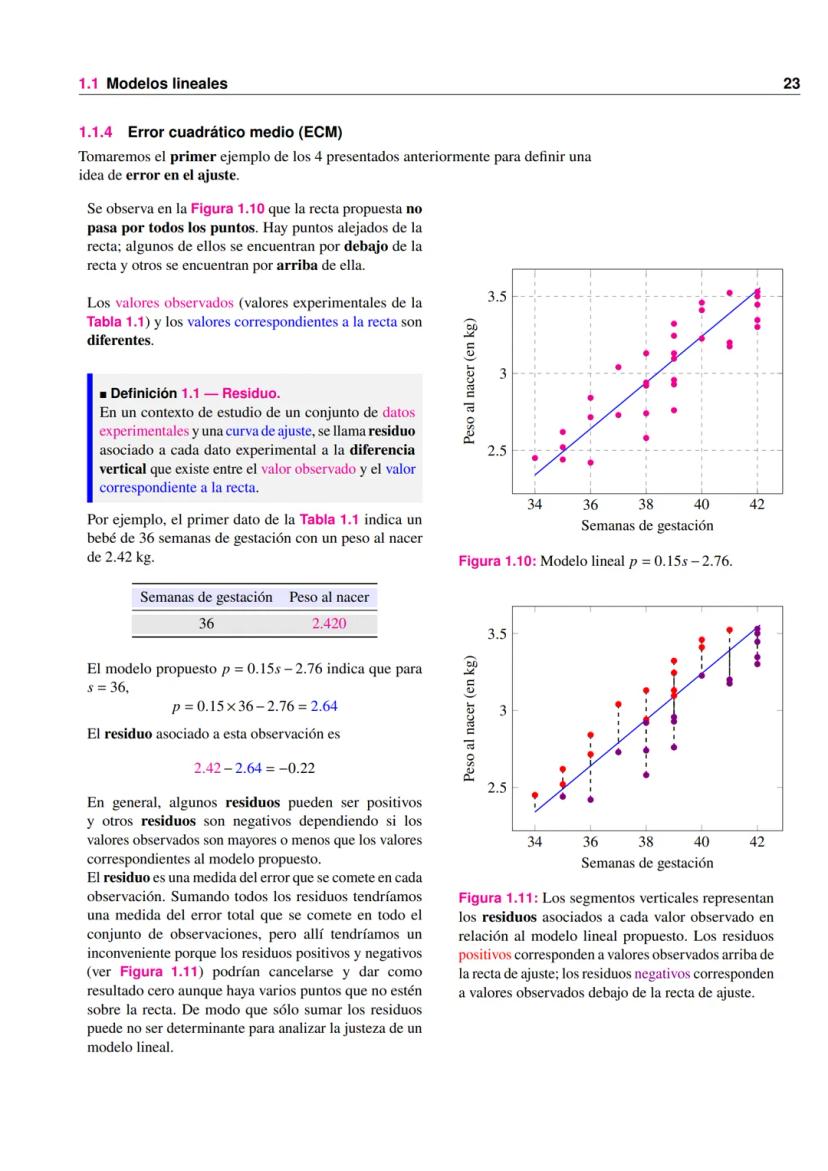
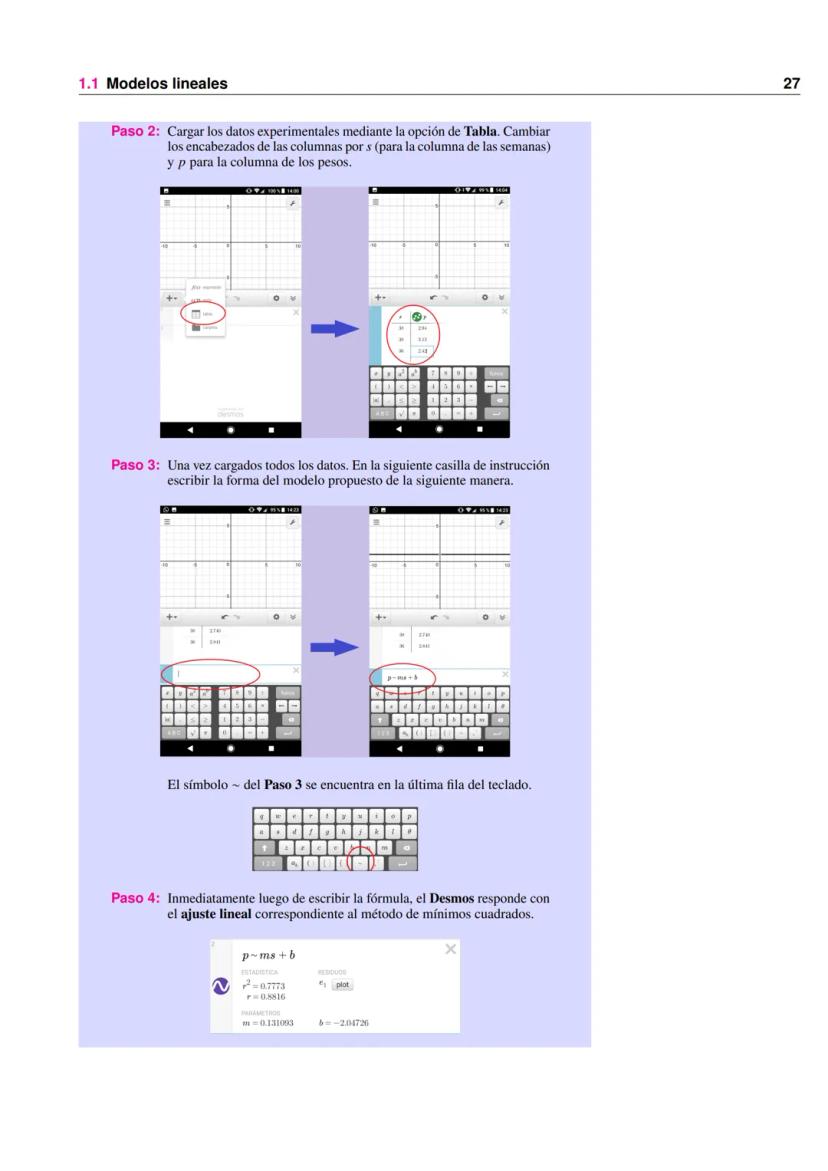
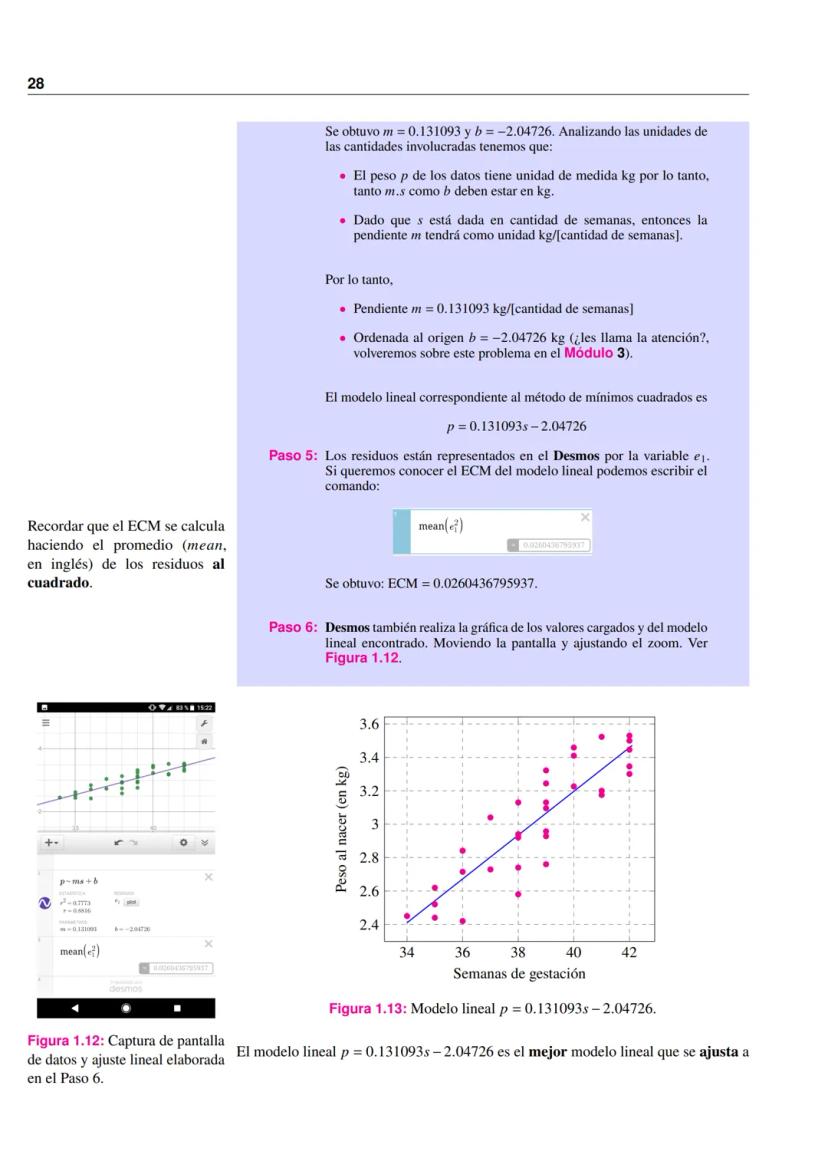
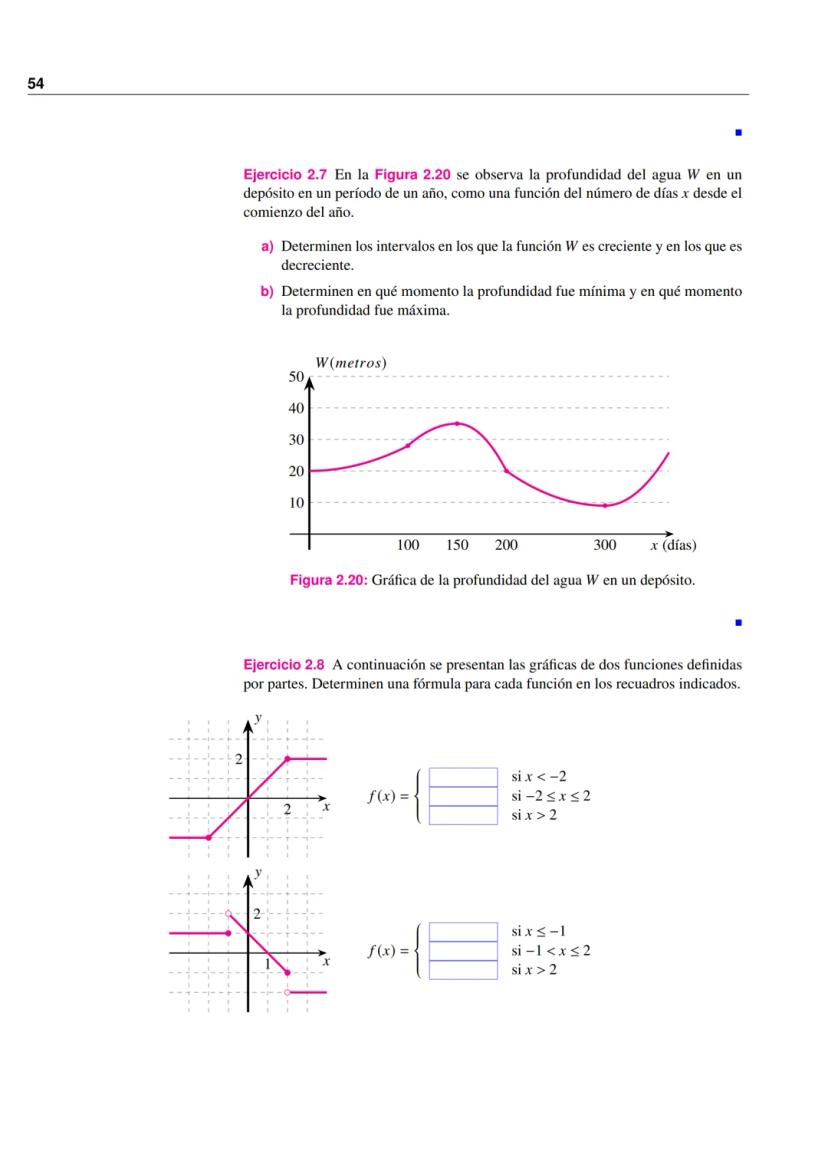
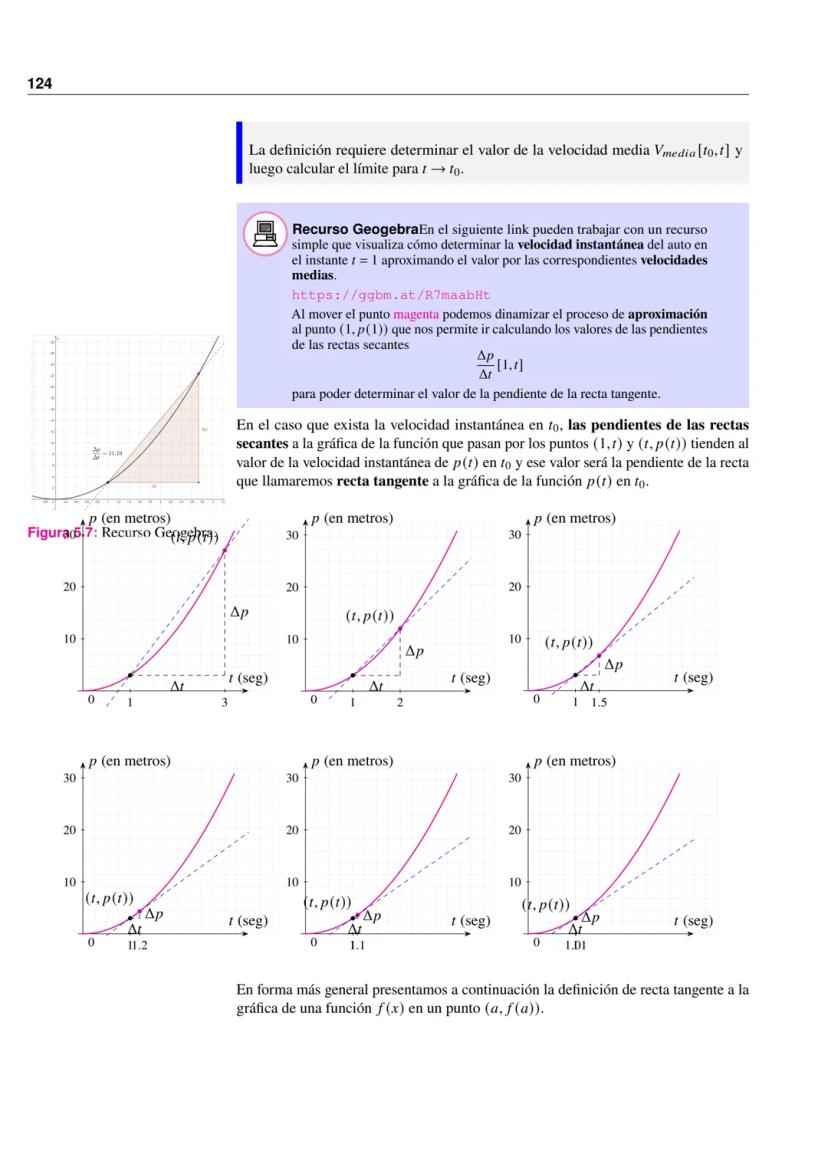
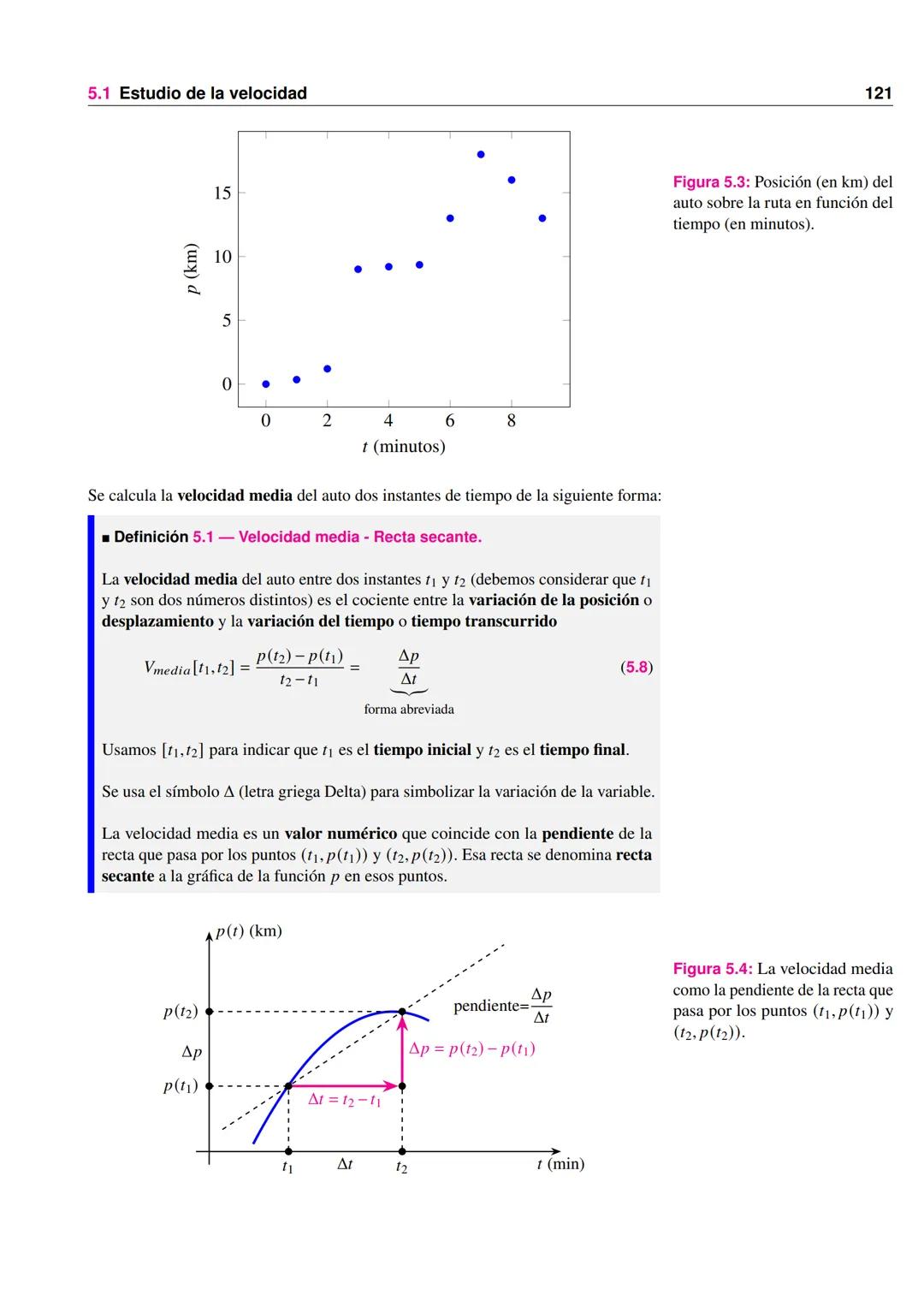
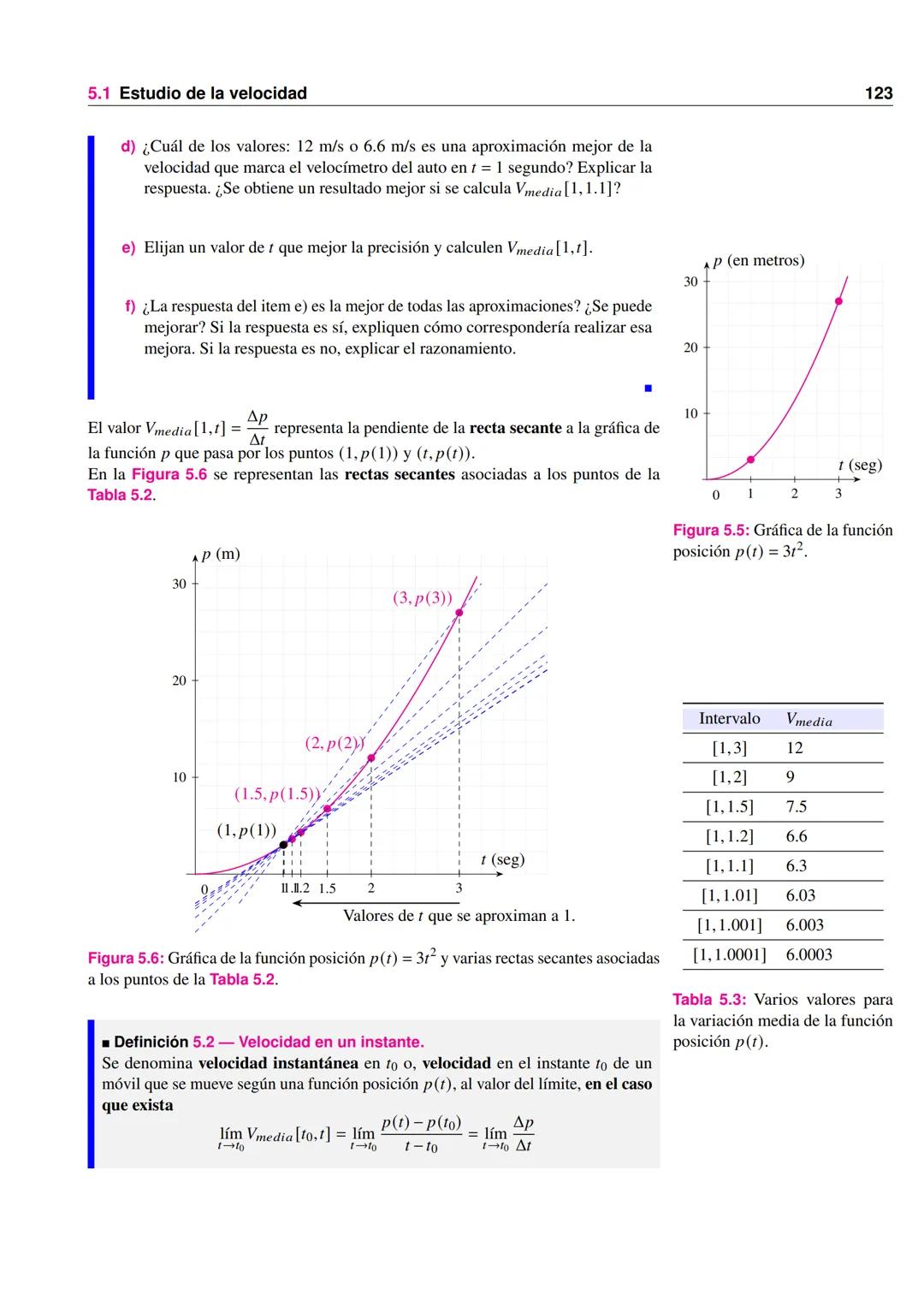
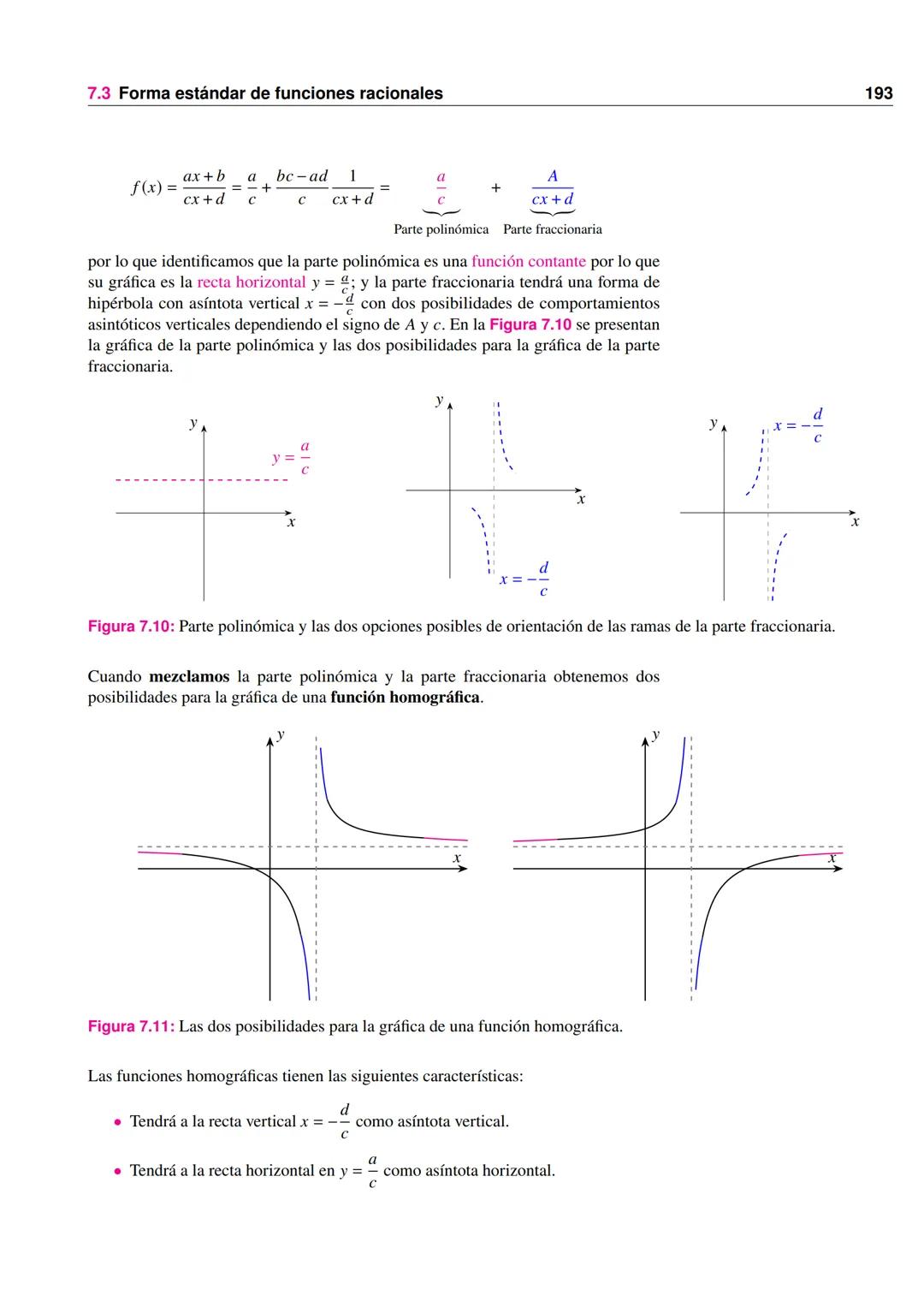
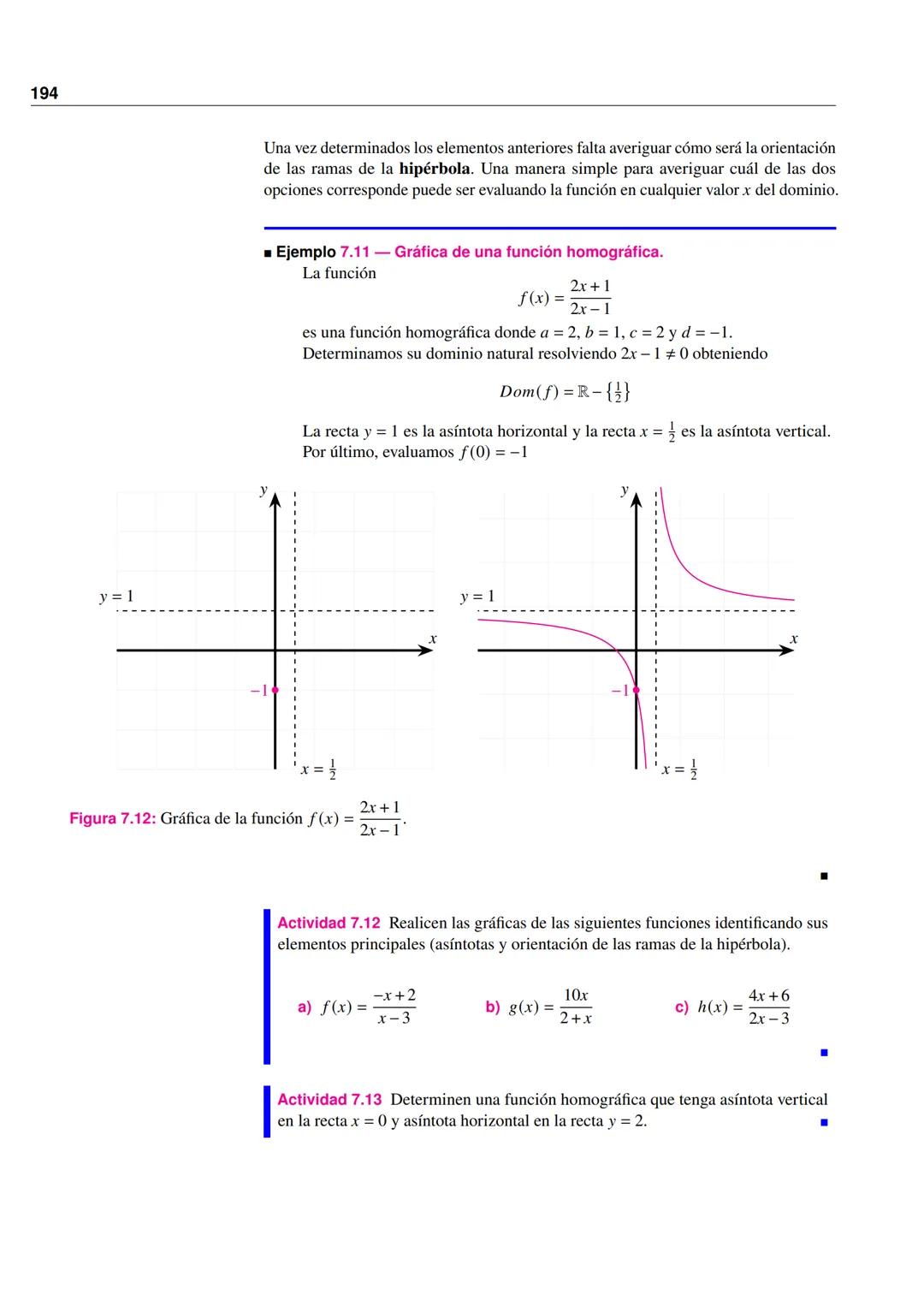
Su gráfica muestra una línea recta con pendiente 50 hasta P = 50, seguida de una línea horizontal en C = 2500.

Evaluación de funciones por partes

Para evaluar una función definida por partes, primero identificamos a qué parte corresponde el valor de entrada, y luego aplicamos la fórmula correspondiente.

Por ejemplo, para la función:

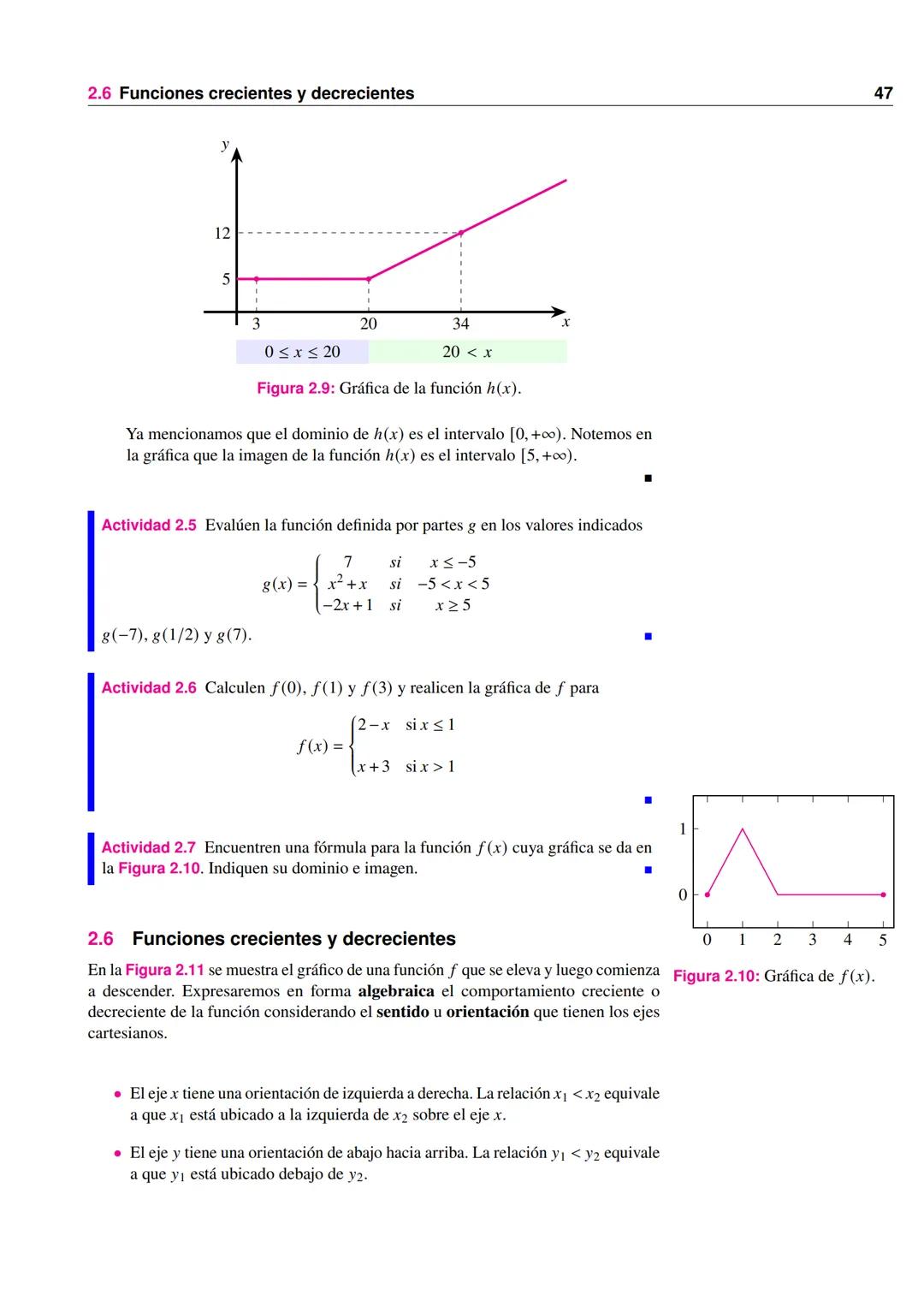
$$h(x) = \begin{cases} 5 & \text{si } 0 \leq x \leq 20 \ 5 + \frac{1}{2}$x-20$ & \text{si } x > 20 \end{cases}$$

Tendríamos:

• h(3) = 5, porque 3 está en el intervalo $0,20$
• h(20) = 5, porque 20 está en el intervalo $0,20$
• h(24) = 5 + 0.5(24-20) = 7, porque 24 > 20

📌 Aplicación: Las funciones definidas por partes son fundamentales en modelos económicos, físicos y médicos donde los comportamientos cambian según umbrales específicos.

Crecimiento, Decrecimiento y Valores Extremos

Las funciones pueden tener comportamientos de crecimiento o decrecimiento en diferentes partes de su dominio.

Funciones crecientes y decrecientes

Una función f es creciente en un intervalo I si para cualquier x₁ < x₂ en I, se cumple que f(x₁) ≤ f(x₂).

Una función f es decreciente en un intervalo I si para cualquier x₁ < x₂ en I, se cumple que f(x₁) ≥ f(x₂).

Por ejemplo, la función f(x) = x² es:

• Decreciente en el intervalo (-∞,0]
• Creciente en el intervalo [0,+∞)

Valores máximos y mínimos

Los valores máximos y mínimos de una función son de interés porque marcan situaciones extremas en el fenómeno estudiado.

Valores extremos absolutos:

• Valor máximo absoluto: f(c) es el valor máximo absoluto si f(c) ≥ f(x) para todo x en el dominio
• Valor mínimo absoluto: f(c) es el valor mínimo absoluto si f(c) ≤ f(x) para todo x en el dominio

Valores extremos locales:

• Valor máximo local: f(c) es un máximo local si f(c) ≥ f(x) cuando x está cerca de c
• Valor mínimo local: f(c) es un mínimo local si f(c) ≤ f(x) cuando x está cerca de c

📌 Aplicaciones: Identificar extremos es crucial en problemas de optimización, como maximizar rendimiento, minimizar costos, o encontrar puntos críticos en mediciones fisiológicas como un electrocardiograma.