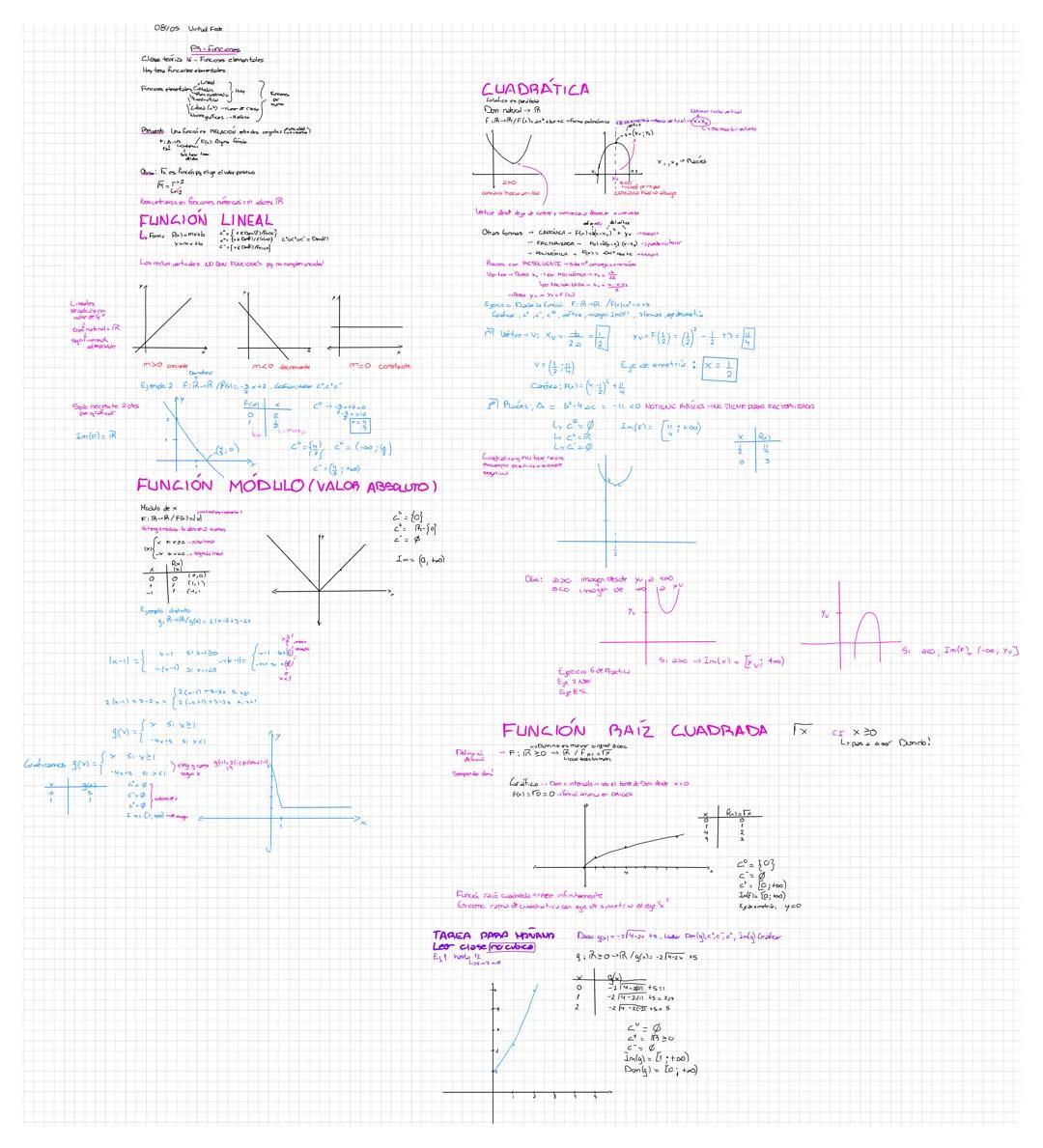
Funciones Elementales
Las funciones elementales son los bloques básicos con los que construimos modelos matemáticos más complejos. Cada una tiene características únicas que debés conocer.
La función lineal se representa como una línea recta en el plano cartesiano. Su fórmula puede expresarse de diferentes formas, pero siempre mantiene una tasa de cambio constante. Es la función más simple y aparece en problemas de movimiento uniforme, costos fijos y variables, entre otros.
La función cuadrática tiene forma de parábola y es esencial para modelar trayectorias de proyectiles o problemas de optimización. Sus valores pueden crecer o decrecer rápidamente dependiendo del signo del coeficiente principal.
💡 Consejo clave: Recordá que en la función módulo (valor absoluto), el punto (0,0) es un vértice que marca un "cambio de dirección" en la gráfica, creando esa característica forma de "V".
La función módulo o valor absoluto se caracteriza por su forma de "V" con vértice en el origen (0,0). Transforma cualquier número negativo en positivo manteniendo iguales los positivos. El dominio es todos los reales ℝ, mientras que su imagen son los números no negativos [0, +∞).
La función raíz cuadrada tiene dominio [0, +∞) e imagen [0, +∞), ya que solo podemos calcular la raíz cuadrada de números no negativos. Su gráfica comienza en el origen y crece cada vez más lentamente, lo que la hace útil en problemas donde el crecimiento se desacelera con el tiempo.
Para el próximo encuentro, la tarea incluye leer sobre la función cúbica. Recordá también las propiedades: g(x) = fx−2 implica un desplazamiento horizontal de la función original.