Conjuntos Numéricos y Axiomas Fundamentales

El conjunto de los números naturales (N) fue el primer sistema numérico creado por la humanidad. Se caracteriza por tener un primer elemento (el 1), ser infinito y discreto. En este conjunto siempre podemos sumar y multiplicar, pero para restar y dividir necesitamos restricciones.

A diferencia de los números naturales, los números enteros (Z) no tienen primer ni último elemento. Cada entero tiene sucesor y antecesor, y el conjunto mantiene las características de ser discreto y ordenado.

Los números racionales (Q) se expresan como cocientes de dos números enteros $\frac{a}{b}$ donde $a, b \in Z$ y $b \neq 0$. Este conjunto es infinito, sin primer ni último elemento, pero a diferencia de Z, es denso - entre dos racionales siempre existe otro racional.

💡 Concepto clave: Un conjunto es denso cuando entre dos elementos cualesquiera siempre podemos encontrar otro elemento del mismo conjunto. Esta propiedad fundamental diferencia a los números racionales de los números naturales y enteros.

Finalmente, al unir los números racionales (Q) con los irracionales (I), obtenemos los números reales $R = Q ∪ I$. Los reales forman un cuerpo ordenado y completo, con propiedades que estudiaremos en detalle.

La verdadera potencia de las matemáticas está en la abstracción. Al entender las propiedades fundamentales de estos conjuntos, desarrollarás una base sólida para todo el análisis matemático que sigue.

El Sistema Axiomático de los Números Reales

Los números reales forman un sistema axiomático completo que se caracteriza como un cuerpo ordenado. Para entender este sistema necesitamos conocer sus componentes fundamentales.

Conceptos Primitivos

• R: Conjunto no vacío cuyos elementos llamamos números reales
• R⁺: Conjunto de números reales positivos
• Dos operaciones fundamentales: suma (+) y producto (·)

Propiedades de la Igualdad

Para todo a, b, c ∈ R:

• Reflexiva: a = a
• Simétrica: Si a = b entonces b = a
• Transitiva: Si a = b y b = c entonces a = c
• Compatibilidad con operaciones: Si a = b entonces a + c = b + c y a · c = b · c

Propiedades de la Suma y el Producto

La suma en R cumple las propiedades de cierre, asociatividad, conmutatividad, existencia de elemento neutro (0) y elemento opuesto $-a$.

💡 Para recordar: Los números reales con la suma forman un grupo abeliano, mientras que R - {0} con el producto también es un grupo abeliano. La combinación de ambas estructuras con la propiedad distributiva da lugar a un cuerpo.

El producto cumple propiedades similares: cierre, asociatividad, conmutatividad, existencia de elemento neutro (1) y elemento inverso (a⁻¹ para todo a ≠ 0).

La propiedad distributiva conecta ambas operaciones: a · $b + c$ = a · b + a · c.

Estos axiomas y propiedades pueden parecer abstractos ahora, pero son las reglas fundamentales que garantizan el funcionamiento de todo el cálculo. Cuando resuelvas ecuaciones o calcules límites, estarás aplicando estas propiedades constantemente, aunque no siempre de manera explícita.

Axiomas de Orden y Valor Absoluto

Axiomas de Orden

Los axiomas de orden nos permiten definir la clase positiva de los números reales (R⁺) y comparar cualquier par de números reales.

1. Axioma de Clausura: La suma y el producto de números positivos siempre son positivos
2. Ley de Tricotomía: Para todo a ∈ R: a = 0 o a ∈ R⁺ o -a ∈ R⁺

A partir de estos axiomas, podemos definir las relaciones "mayor que" y "menor que":

• a > b si y solo si a - b ∈ R⁺
• a < b si y solo si b > a

Estas relaciones cumplen propiedades importantes:

• Si a < b entonces a + c < b + c (monotonía de la suma)
• Si a < b y c > 0 entonces a·c < b·c
• Si a < b y c < 0 entonces a·c > b·c

💡 Aplicación práctica: Estas propiedades de orden son las que te permiten resolver desigualdades manteniendo el sentido de la desigualdad al sumar términos o al multiplicar por valores positivos, y cambiando el sentido cuando multiplicas por valores negativos.

Valor Absoluto

El valor absoluto de un número real u, denotado |u|, se define como:

|u| = { u, si u ≥ 0 -u, si u < 0 }

Geométricamente, representa la distancia de u al cero en la recta numérica.

Entre sus propiedades más útiles encontramos:

• |u| = √(u²)
• |u| ≥ 0 para todo u ∈ R
• |u| = |-u|
• |u·v| = |u|·|v|
• |u+v| ≤ |u| + |v| (desigualdad triangular)

La interpretación del valor absoluto como distancia es fundamental para entender conceptos posteriores como límites y continuidad.

Distancia, Intervalos y Entornos en los Reales

Distancia entre Números Reales

La distancia entre dos números reales s y t se define como:

d(s,t) = |t-s| = |s-t|

Este concepto es fundamental para entender la topología de la recta real.

Intervalos Acotados

Los intervalos son conjuntos de puntos contiguos de la recta real. Pueden ser:

• Intervalo cerrado: $a;b$ = {x ∈ R | a ≤ x ≤ b}
• Intervalo abierto: (a;b) = {x ∈ R | a < x < b}
• Intervalos semiabiertos: $a;b) = {x ∈ R | a ≤ x < b} y (a;b$ = {x ∈ R | a < x ≤ b}

La amplitud de cualquier intervalo es d(a,b) = |b-a|.

Intervalos No Acotados

Los símbolos +∞ y -∞ no representan números, sino conceptos que nos permiten definir:

• [a;+∞) = {x ∈ R | x ≥ a}
• $a;+∞$ = {x ∈ R | x > a}
• (-∞;a] = {x ∈ R | x ≤ a}
• $-∞;a$ = {x ∈ R | x < a}

💡 Observación importante: Aunque usamos los símbolos +∞ y -∞, estos no son números reales y no podemos operar con ellos como tales. Son simplemente una notación para expresar intervalos que se extienden indefinidamente.

Entornos

Un entorno de centro c y radio r se define como:

E(c,r) = $c-r; c+r$ = {x ∈ R | |x-c| < r}

Un entorno reducido excluye el centro:

E*(c,r) = E(c,r) - {c} = {x ∈ R | 0 < |x-c| < r}

Los entornos son herramientas esenciales para definir conceptos como límites y continuidad en análisis matemático.

Cotas y Supremos e Ínfimos de Conjuntos

Cuando trabajamos con conjuntos de números reales, es fundamental poder hablar sobre sus límites superiores e inferiores. Estos conceptos serán la base para entender límites de funciones más adelante.

Cotas de un Conjunto

• Un número c es cota superior de un conjunto A si para todo x ∈ A, se cumple x ≤ c.
• Un número c es cota inferior de un conjunto A si para todo x ∈ A, se cumple x ≥ c.

Elementos Extremos

• Un número M es elemento máximo de A si M es cota superior de A y M ∈ A.
• Un número m es elemento mínimo de A si m es cota inferior de A y m ∈ A.

💡 Propiedad importante: Si existe un máximo (o mínimo) para un conjunto, este es único. No todos los conjuntos tienen máximo o mínimo, especialmente si son conjuntos infinitos o no acotados.

Supremo e Ínfimo

• El supremo (Sup) de un conjunto A es la menor de todas sus cotas superiores.
• El ínfimo (Inf) de un conjunto A es la mayor de todas sus cotas inferiores.

Estos conceptos son más generales que el máximo y mínimo, ya que existen incluso para conjuntos que no tienen máximo o mínimo.

Axioma de Completitud

Uno de los axiomas fundamentales de los números reales establece que: Todo conjunto no vacío de números reales acotado superiormente (inferiormente) admite supremo (ínfimo).

Este axioma es lo que distingue a los números reales de los racionales y es esencial para el desarrollo del cálculo. Gracias a él podemos trabajar con límites y garantizar la existencia de ciertos valores cruciales.

Para ilustrar estos conceptos, considera el conjunto A = (-4; 3]:

• Sus cotas superiores son todos los números mayores o iguales a 3
• El supremo (y máximo) de A es 3
• Sus cotas inferiores son todos los números menores o iguales a -4
• El ínfimo de A es -4, pero no es un mínimo porque -4 ∉ A

Introducción a las Funciones

El concepto de función es quizás la idea central en matemáticas. Una función establece una relación entre elementos de dos conjuntos, asignando a cada elemento del primer conjunto exactamente un elemento del segundo conjunto.

Evolución Histórica del Concepto

El concepto de función ha evolucionado a lo largo de los siglos:

• Los babilonios ya manejaban relaciones específicas (como tablas de cuadrados)
• Descartes (1637) introdujo el concepto para simbolizar potencias
• Euler (1706-1783) describió funciones como relaciones entre variables y constantes
• Dirichlet (1805-1859) las describió como reglas de correspondencia
• Goursat (1923) dio la definición moderna: "y es función de x si a cada x le corresponde un único y"

Definición Formal de Función

Sean A ≠ ∅ y B ≠ ∅ dos conjuntos. Una función f de A en B es una regla que asocia a cada elemento x del conjunto A un único elemento y del conjunto B.

Simbólicamente: f: A → B, x → y = f(x)

Para que f sea función debe cumplir:

1. Condición de existencia: ∀x ∈ A, ∃y ∈ B / y = f(x)
2. Condición de unicidad: ∀x ∈ A, ∀y,z ∈ B: $(x,y) ∈ f ∧ (x,z) ∈ f$ ⇒ y = z

💡 Nota importante: Una función puede verse como un conjunto de pares ordenados (x,y) donde no hay dos pares con el mismo primer elemento. Esta perspectiva te ayudará a entender mejor conceptos como la inversa de una función.

Dominio y Recorrido

• El dominio de una función f (denotado D[f]) es el conjunto formado por los primeros elementos de los pares ordenados de f.
• El recorrido o rango de una función (denotado R[f]) es el conjunto formado por los segundos elementos de los pares ordenados de f.

Entender bien estos conceptos es fundamental, ya que muchos problemas de cálculo consisten en determinar correctamente dominios y recorridos de funciones.

Representación de Funciones y Distancia en el Plano

Plano Cartesiano

Un plano cartesiano es un sistema que usa coordenadas para determinar la posición de puntos. Está formado por:

• El eje X o eje de las abscisas (horizontal)
• El eje Y o eje de las ordenadas (vertical)
• El origen de coordenadas (0,0), donde se intersectan ambos ejes

Cada punto del plano se representa mediante un par ordenado (x,y), donde x es la distancia horizontal desde el origen, e y es la distancia vertical.

Funciones Escalares

Las funciones escalares son aquellas donde tanto el dominio como el codominio son subconjuntos de los números reales. Su dominio es el conjunto de números reales para los cuales la función está definida (tiene sentido).

Gráfica de Funciones Escalares

Una función puede representarse de diversas formas:

• Tabla de valores
• Expresión algebraica
• Gráfico cartesiano
• Diagrama de Venn
• Descripción verbal

La gráfica de una función f es el conjunto de puntos (x,y) del plano cartesiano tales que y = f(x). Simbólicamente: f = {(x,y) ∈ R² | y = f(x), x ∈ D$f$}

💡 Prueba de la línea vertical: Una curva en el plano XY es la gráfica de una función si y solo si ninguna línea vertical corta la curva más de una vez. Esta prueba es una consecuencia directa de la condición de unicidad.

Distancia entre Puntos del Plano

La distancia entre dos puntos A = (x₁,y₁) y B = (x₂,y₂) se define como: d(A,B) = √$(x₂-x₁)² + (y₂-y₁)²$

Esta fórmula, derivada del Teorema de Pitágoras, es fundamental para calcular distancias en el plano y será útil en conceptos como continuidad y diferenciabilidad.

La visualización gráfica de las funciones te permite desarrollar una intuición matemática valiosa. Observar cómo cambia la gráfica cuando modificas la función te ayudará a entender mejor su comportamiento.

Tipos y Clasificación de Funciones

Clasificación por Inyectividad y Sobreyectividad

• Función Inyectiva: Si para cada par de elementos diferentes en el dominio, sus imágenes son diferentes. Formalmente: ∀x₁, x₂ ∈ A: f(x₁) = f(x₂) ⟹ x₁ = x₂

• Función Sobreyectiva: Si todo elemento del codominio tiene al menos una preimagen. Formalmente: ∀y ∈ B, ∃x ∈ A / f(x) = y

• Función Biyectiva: Si es tanto inyectiva como sobreyectiva. En este caso, cada elemento del codominio tiene exactamente una preimagen.

💡 Aplicación práctica: Solo las funciones inyectivas tienen inversa. Esto es crucial cuando necesitas "deshacer" una función o resolver ecuaciones de la forma f(x) = k.

Igualdad de Funciones

Dos funciones f y g son iguales si:

1. Tienen el mismo dominio: D$f$ = D$g$
2. Para todo x del dominio: f(x) = g(x)

Funciones Elementales

Función Lineal

Definida como f(x) = mx + b, donde:

• m es la pendiente (inclinación de la recta)
• b es la ordenada al origen (punto donde la recta corta al eje Y)

Su dominio y recorrido son R.

Casos Especiales de Funciones Lineales

• Función Constante: f(x) = c (pendiente 0)
• Función Identidad: f(x) = x (pendiente 1, ordenada al origen 0)

Otras Funciones Básicas

• Función Valor Absoluto: f(x) = |x|
• Función Signo: Sgn(x) = {1 si x>0, 0 si x=0, -1 si x<0}
• Función Potencial: f(x) = xⁿ para n∈R
• Función Polinómica: P(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀
• Función Racional: R(x) = P(x)/Q(x) donde P y Q son polinomios y Q(x)≠0

Comprender estos tipos básicos te permitirá analizar funciones más complejas descomponiéndolas en componentes más simples.

Funciones por Tramos y Propiedades Especiales

Funciones por Tramos

Las funciones por tramos (o a trozos) están definidas por diferentes fórmulas en distintas partes de su dominio. Se expresan como:

f(x) = { f₁(x) si x ∈ D₁ f₂(x) si x ∈ D₂ ... fₙ(x) si x ∈ Dₙ }

donde D₁ ∪ D₂ ∪ ... ∪ Dₙ = D$f$

Estas funciones son importantes porque permiten modelar situaciones con diferentes comportamientos en distintos intervalos, como tarifas por tramos o funciones con discontinuidades.

Funciones Pares e Impares

• Función Par: Cumple f$-x$ = f(x) para todo x en su dominio. Su gráfica es simétrica respecto al eje Y. Ejemplos: f(x) = x², f(x) = |x|, f(x) = cos(x)

• Función Impar: Cumple f$-x$ = -f(x) para todo x en su dominio. Su gráfica es simétrica respecto al origen. Ejemplos: f(x) = x³, f(x) = sen(x), f(x) = tan(x)

💡 Recordatorio útil: La función constante $excepto f(x)=0$ es par, mientras que la función identidad es impar. Esto te ayudará a determinar rápidamente si otras funciones son pares o impares.

Operaciones con Funciones

Si f y g son funciones, podemos definir:

• Suma: $f+g$(x) = f(x) + g(x)
• Resta: $f-g$(x) = f(x) - g(x)
• Producto: (f·g)(x) = f(x) · g(x)
• Cociente: $f/g$(x) = f(x)/g(x) (donde g(x)≠0)
• Producto por escalar: (c·f)(x) = c · f(x) para c∈R

Estas operaciones cumplen propiedades similares a las operaciones con números reales (conmutatividad, asociatividad, distributividad), lo que facilita su manipulación algebraica.

El estudio de estas propiedades te permitirá simplificar expresiones complejas y analizar el comportamiento de funciones compuestas.

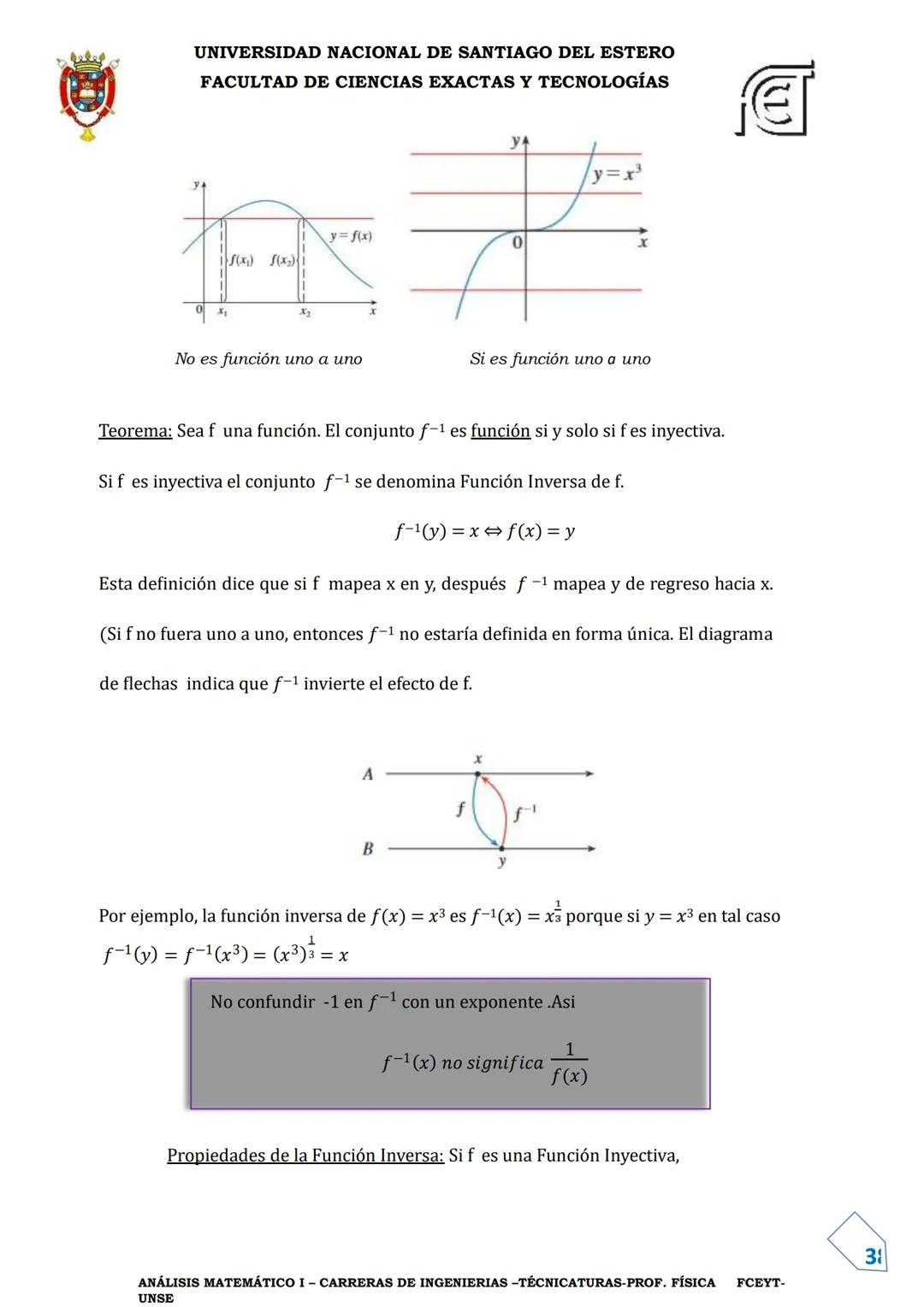
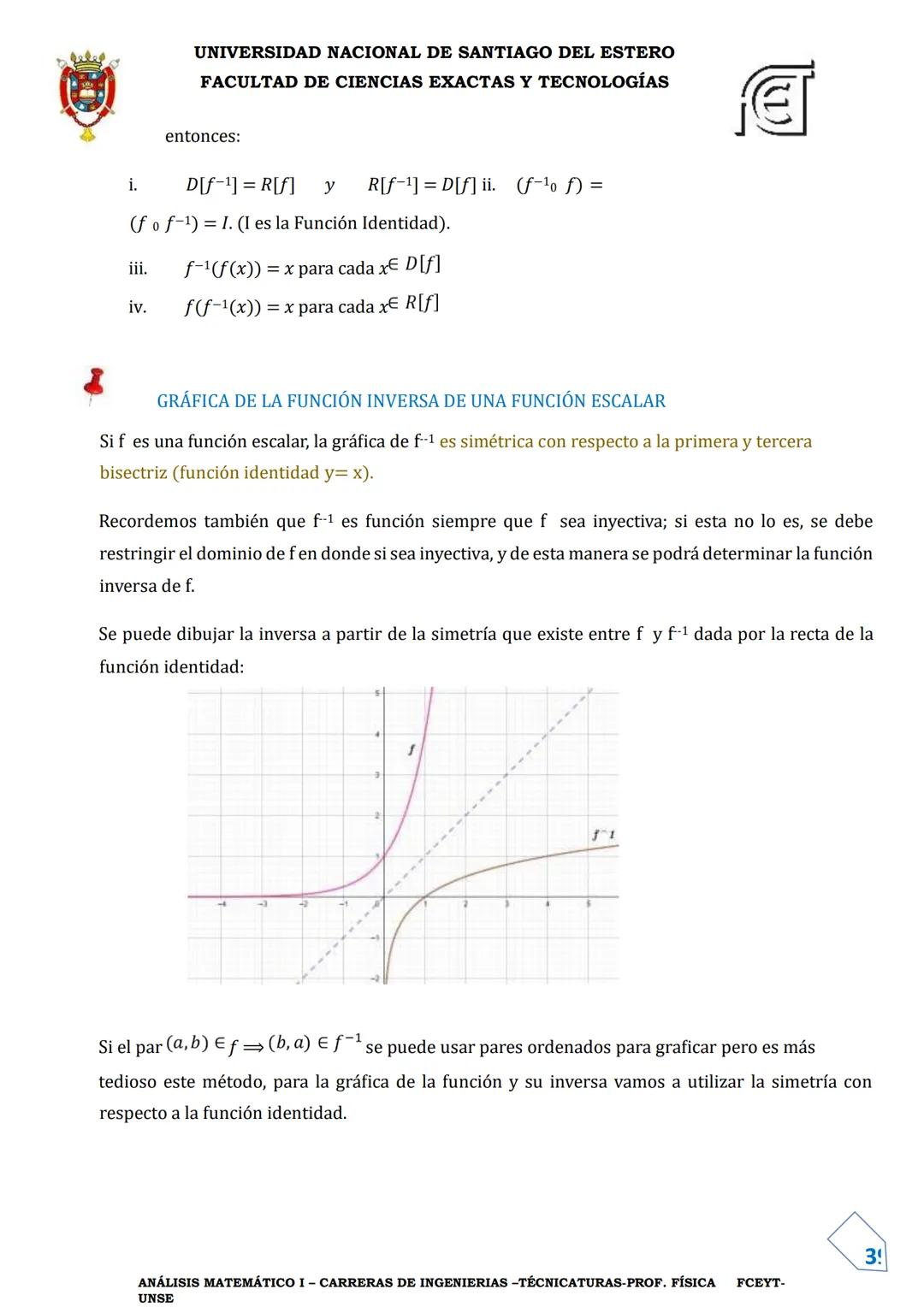
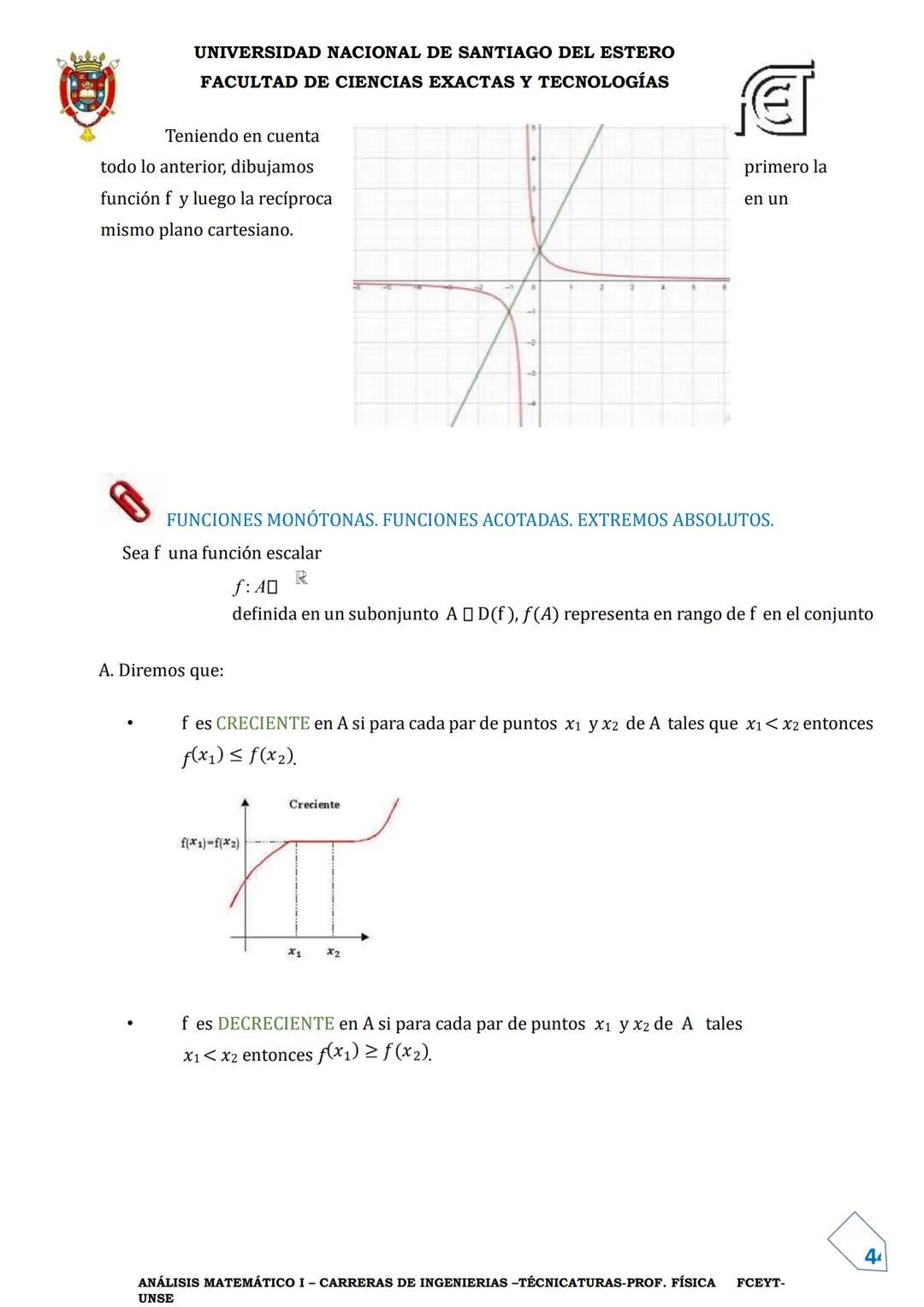
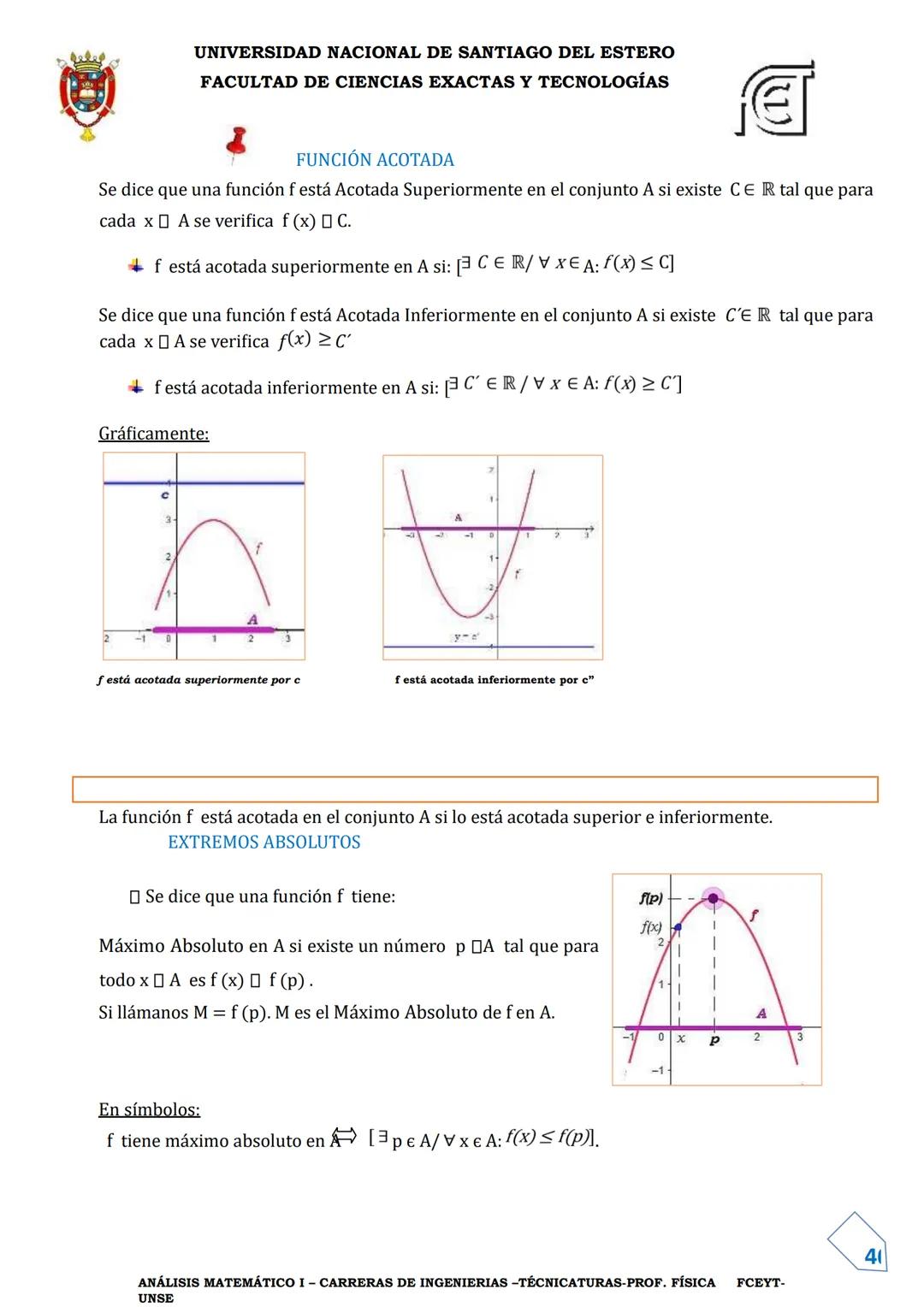
Composición de Funciones e Inversa

Composición de Funciones

Dadas dos funciones f y g, podemos definir la función compuesta g∘f (leída "g compuesta con f") como:

(g∘f)(x) = g$f(x)$ para todo x en D$g∘f$

donde D$g∘f$ = {x | x∈D$f$ y f(x)∈D$g$}

Para realizar la composición, el recorrido de la primera función debe estar incluido (o al menos intersecarse) con el dominio de la segunda.

Propiedades importantes:

• La composición no es conmutativa: generalmente g∘f ≠ f∘g
• La composición sí es asociativa: (h∘g)∘f = h∘(g∘f)

💡 Interpretación práctica: La composición de funciones representa aplicar una función después de otra. Por ejemplo, si f convierte grados a radianes y g calcula el seno, entonces g∘f calcula el seno de un ángulo dado en grados.

Función Inversa

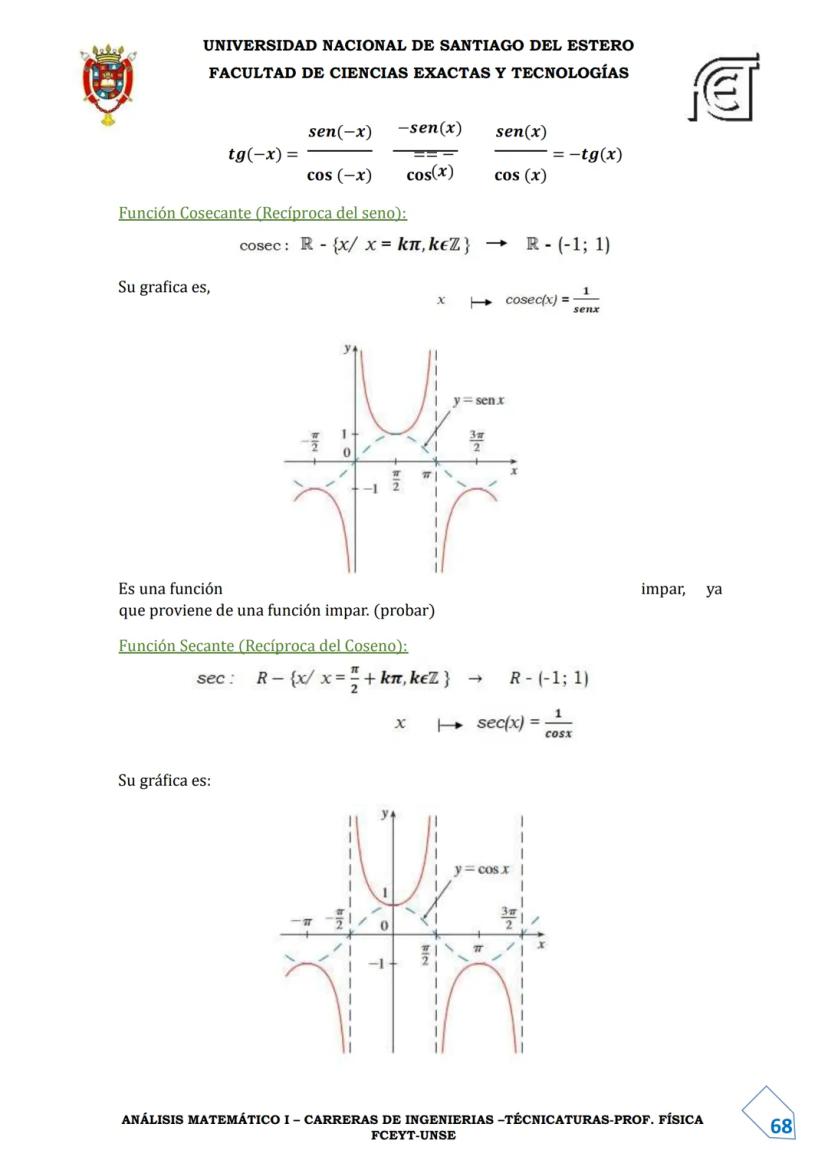
Si f es una función inyectiva, entonces existe su función inversa f⁻¹, que "deshace" lo que f hace:

f⁻¹(y) = x si y solo si f(x) = y

Propiedades de la función inversa:

1. D$f⁻¹$ = R$f$ y R$f⁻¹$ = D$f$
2. (f⁻¹∘f)(x) = x para todo x∈D$f$
3. (f∘f⁻¹)(y) = y para todo y∈R$f$

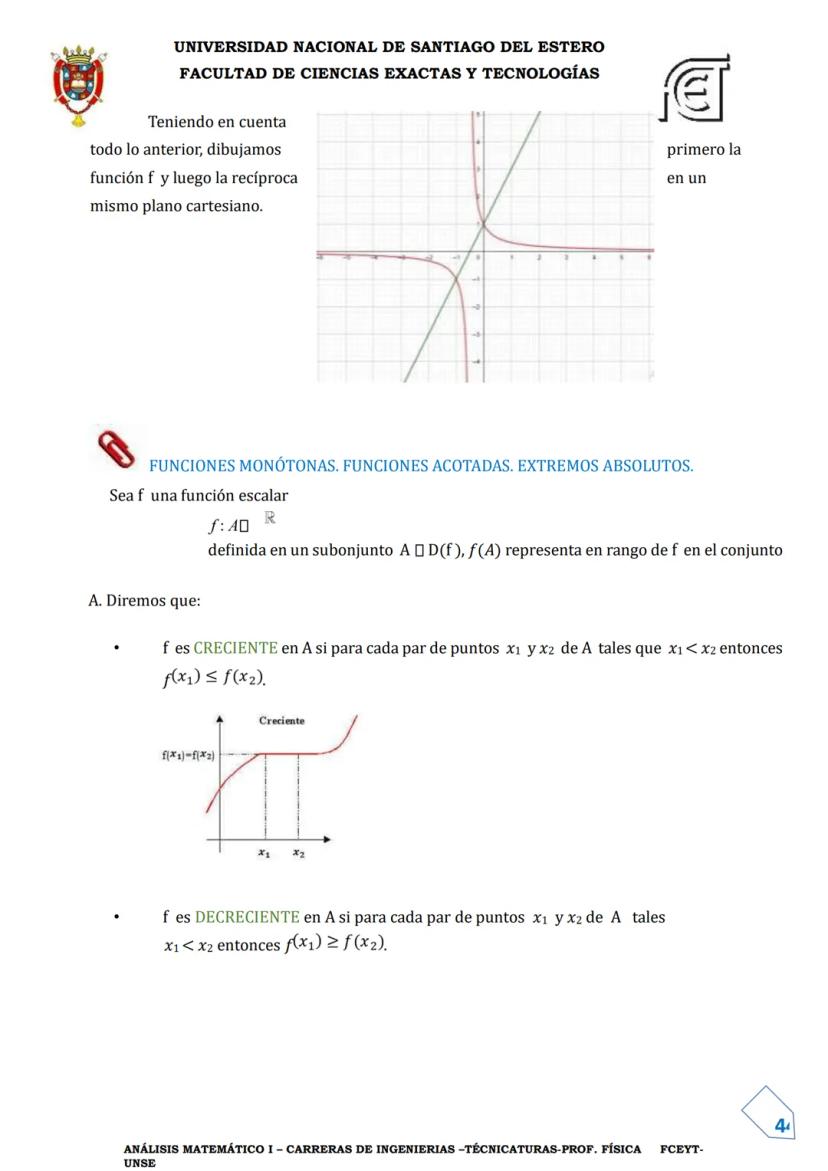
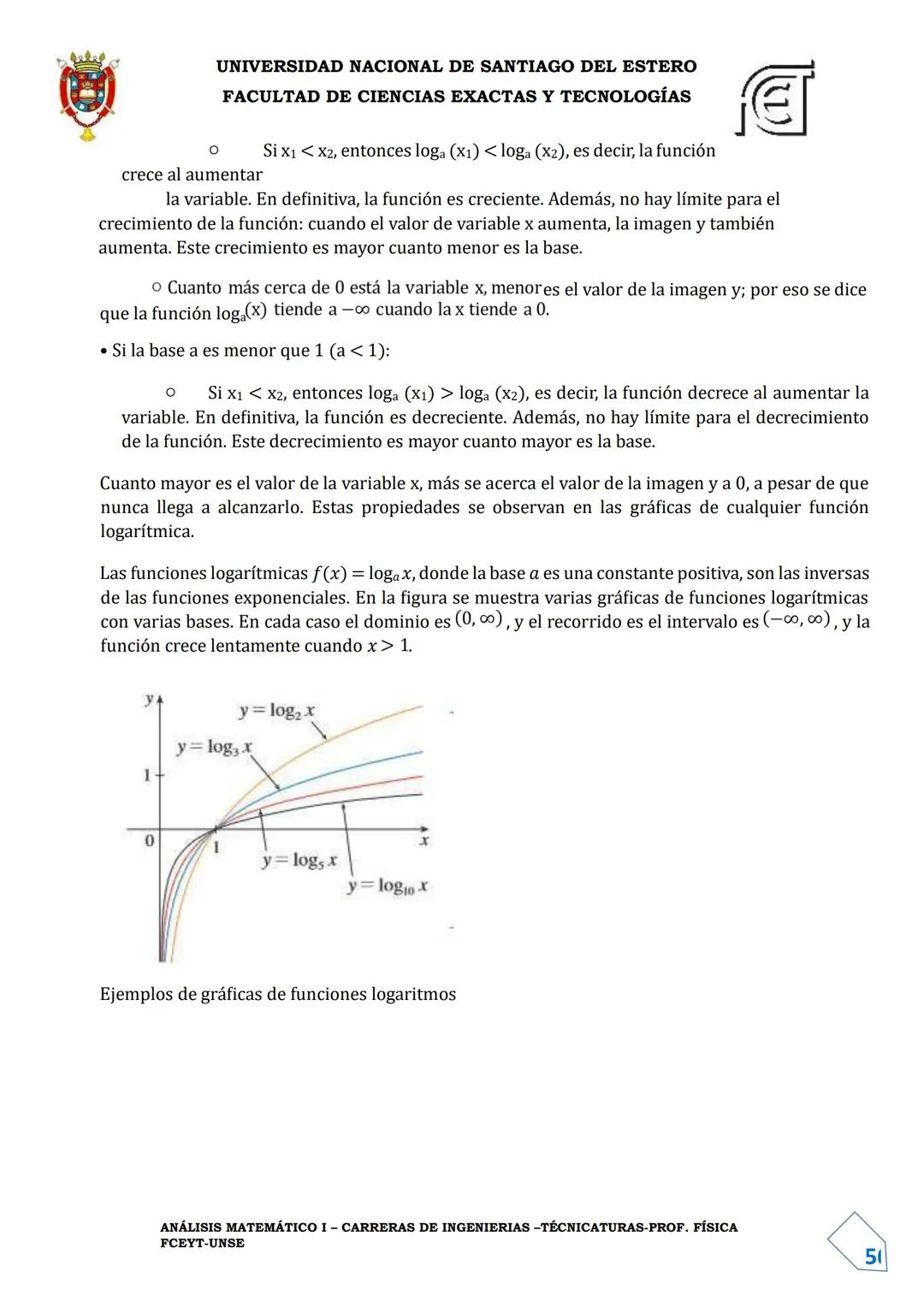
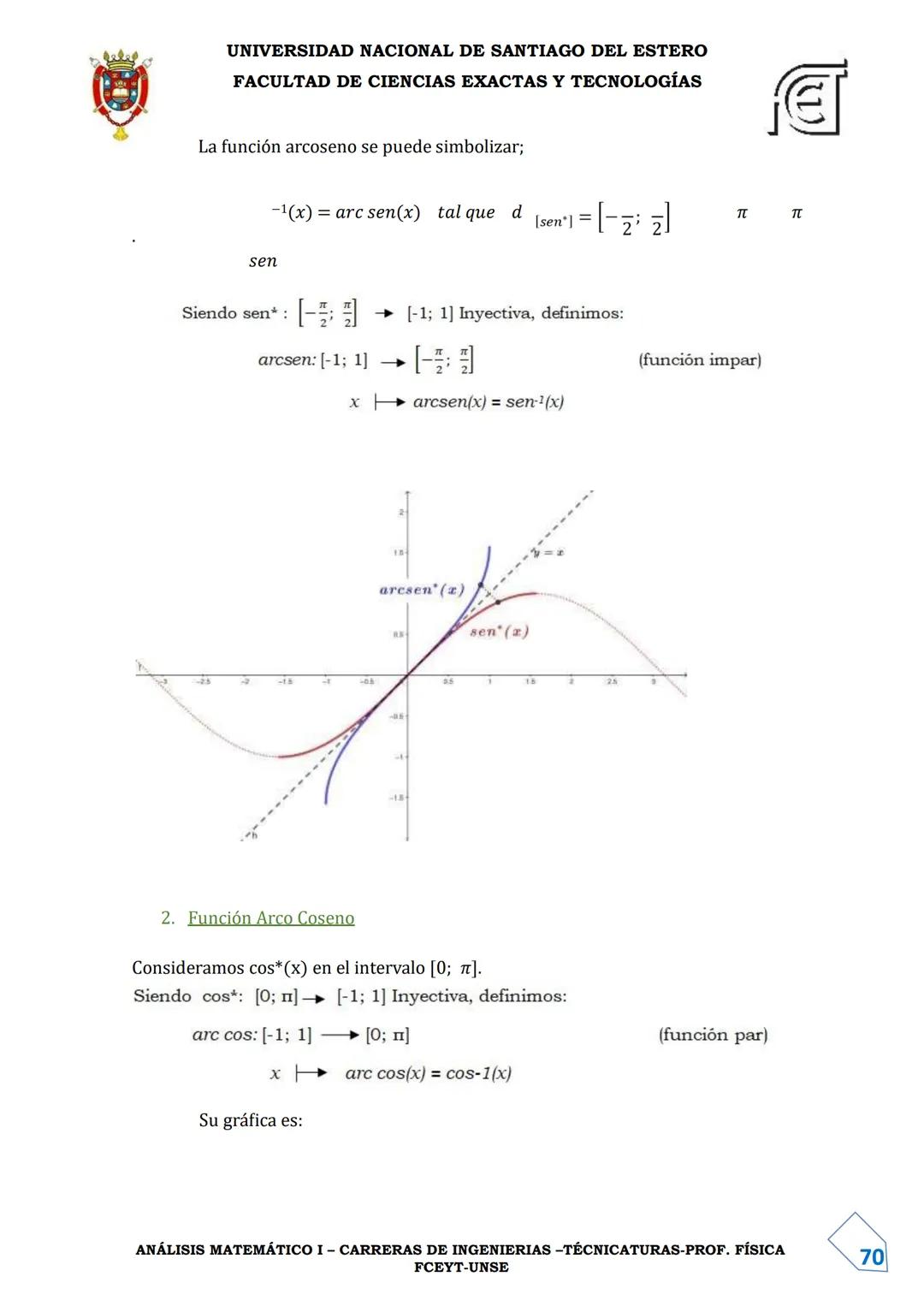
Gráficamente: La gráfica de f⁻¹ es simétrica a la de f respecto a la recta y = x.

Restricción de una Función

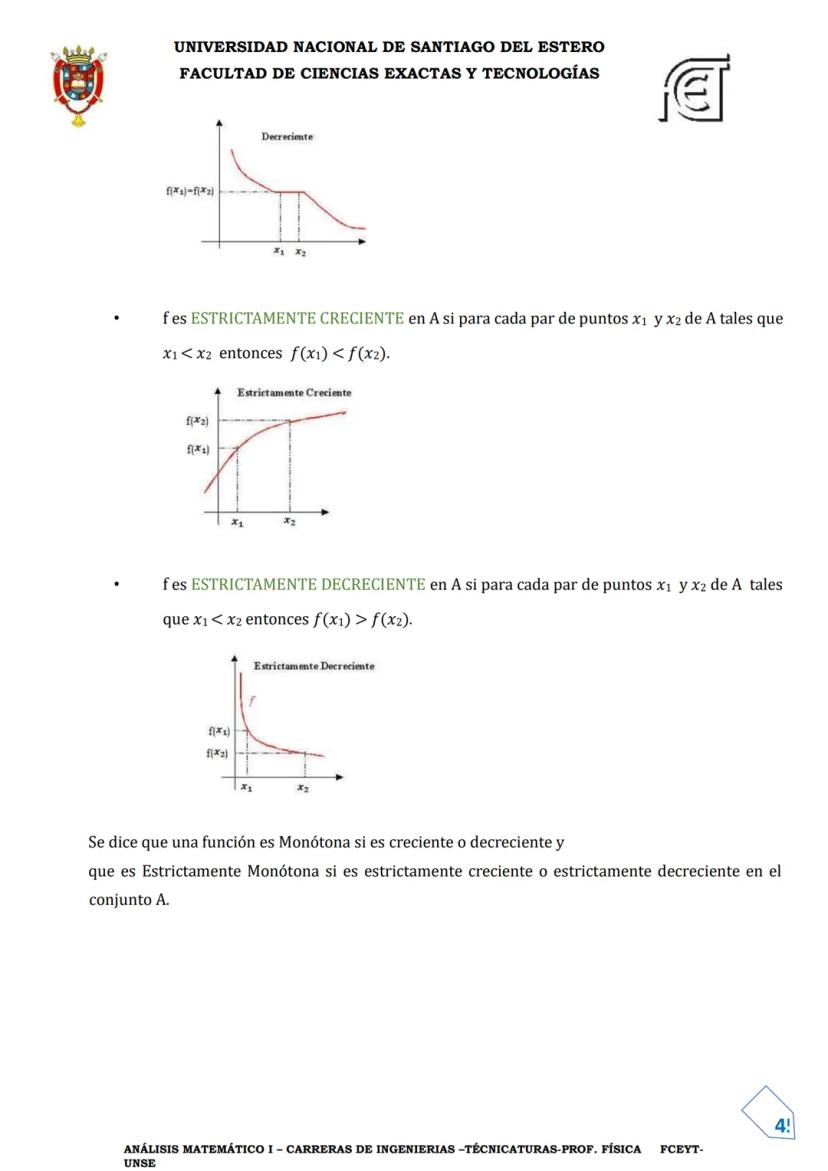
Si una función no es inyectiva, podemos restringir su dominio para obtener una función inyectiva y así poder definir su inversa en ese subdominio.

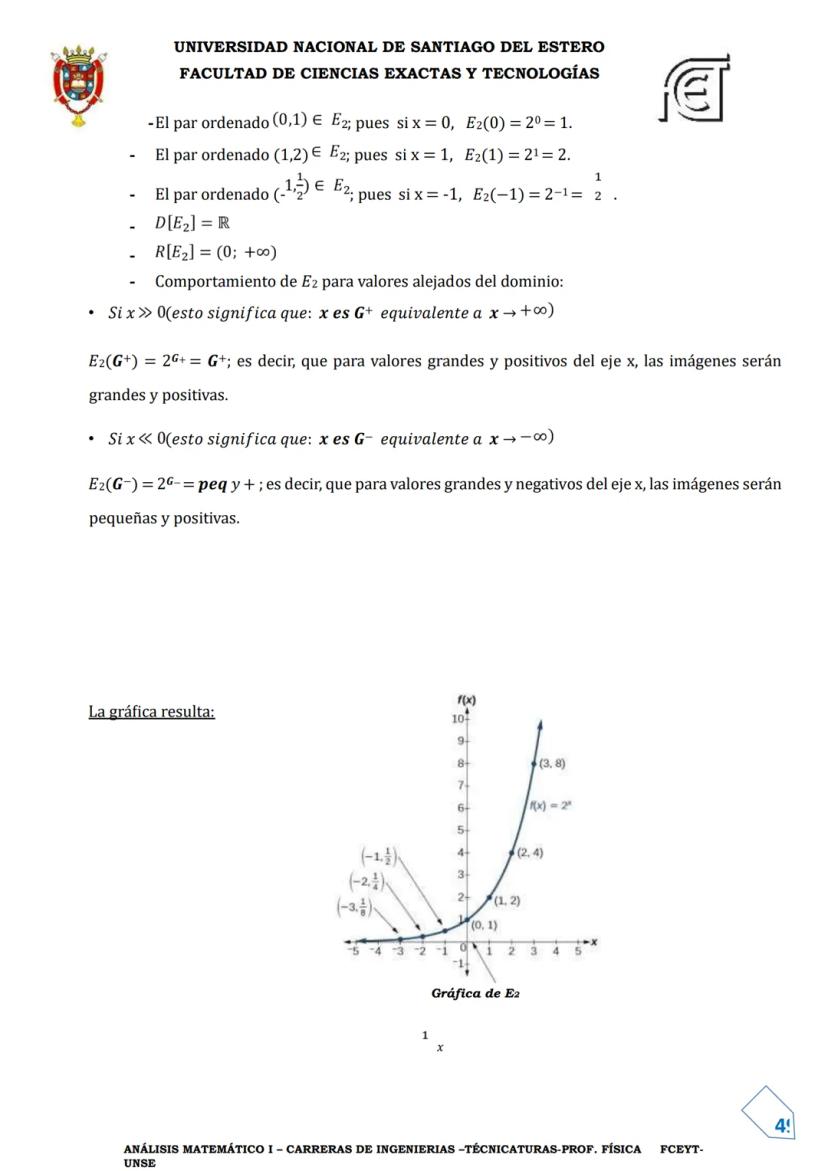
Por ejemplo, f(x) = x² con D$f$ = R no es inyectiva, pero si restringimos su dominio a [0,+∞), obtenemos una función inyectiva cuya inversa es f⁻¹(x) = √x.

Entender bien la composición e inversión de funciones es fundamental para resolver ecuaciones y modelar procesos reversibles en ciencias e ingeniería.