Sistemas de Ecuaciones Lineales: Fundamentos

Un sistema de ecuaciones lineales es un conjunto de ecuaciones donde cada variable aparece elevada a la potencia 1 y no hay productos entre variables.

Una ecuación lineal con n variables se escribe como: a₁x₁ + a₂x₂ + ... + aₙxₙ = b

En el espacio bidimensional (R²), una ecuación lineal representa una recta: a₁x + a₂y = b

En el espacio tridimensional (R³), representa un plano: a₁x + a₂y + a₃z = b

Para que una ecuación sea lineal debe cumplir estas condiciones:

• No debe tener productos entre variables
• Las variables no aparecen en raíces o funciones trigonométricas

Según sus soluciones, los sistemas pueden clasificarse como:

• Sistema compatible determinado: tiene una única solución
• Sistema compatible indeterminado: tiene infinitas soluciones
• Sistema incompatible: no tiene solución (inconsistente)

💡 Consejo útil: Para identificar rápidamente el tipo de sistema, observa la forma escalonada de su matriz. Si aparece una fila con todos ceros excepto en la última columna, el sistema es incompatible.

La representación matricial de un sistema tiene la forma Ax = b, donde A es la matriz de coeficientes, x el vector de incógnitas y b el vector de términos independientes.

Matrices y Forma Escalonada

Una matriz es un arreglo rectangular de números organizados en filas (renglones) y columnas. La matriz aumentada de un sistema incluye tanto los coeficientes como los términos independientes.

La forma escalonada reducida por renglones (o forma de pivotes) de una matriz debe cumplir:

• Los renglones con todos ceros aparecen en la parte inferior
• El primer 1 de cada renglón está más a la derecha que el primer 1 del renglón anterior
• El primer número distinto de cero en cada renglón no nulo es 1 (pivote)
• Cada columna que contiene un pivote tiene ceros en el resto de posiciones

Para transformar una matriz a forma escalonada usamos operaciones elementales:

1. Multiplicar un renglón por una constante distinta de cero
2. Intercambiar dos renglones
3. Sumar un múltiplo de un renglón a otro renglón

Existen dos principales métodos para resolver sistemas:

• Eliminación Gaussiana: transforma la matriz a forma escalonada
• Eliminación Gauss-Jordan: lleva la matriz a forma escalonada reducida

💡 Dato clave: Un sistema homogéneo $donde b=0$ siempre tiene al menos la solución trivial $x=0$. Si m<n (menos ecuaciones que incógnitas), garantiza infinitas soluciones.

Según sus características, los sistemas pueden ser:

• Subdeterminados (m<n): tienen infinitas soluciones
• Sobredeterminados (m>n): pueden no tener solución

Operaciones con Matrices

Las operaciones elementales nos permiten transformar sistemas en otros equivalentes (con las mismas soluciones):

1. Multiplicar una ecuación por una constante no nula
2. Intercambiar dos ecuaciones
3. Sumar un múltiplo de una ecuación a otra

Estas operaciones se representan en notación matricial como:

• R₁ → cR₁ (multiplicar renglón 1 por c)
• R₁ ↔ R₂ (intercambiar renglones 1 y 2)
• R₃ → R₃ + 3R₂ (sumar a renglón 3 el triple del renglón 2)

En la eliminación gaussiana, el objetivo es obtener una matriz escalonada que nos permita encontrar el valor de cada variable mediante sustitución hacia atrás.

La matriz de coeficientes contiene solo los coeficientes de las variables, mientras que la matriz ampliada incluye también los términos independientes:

[a₁₁ a₁₂ ... a₁ₙ | b₁]
[a₂₁ a₂₂ ... a₂ₙ | b₂]
[...               |...]
[aₘ₁ aₘ₂ ... aₘₙ | bₘ]

💡 Truco práctico: Al resolver un sistema, identifica primero los pivotes en la matriz escalonada. Las columnas con pivotes corresponden a las variables principales, mientras que las demás son variables libres a las que puedes asignar parámetros.

Un sistema homogéneo siempre es consistente $tiene al menos la solución trivial x=0$.

Tipos de Sistemas y Matrices

Los sistemas homogéneos $Ax=0$ tienen características especiales:

• Siempre tienen al menos la solución trivial $x=0$
• Si m<n (menos ecuaciones que incógnitas), tienen infinitas soluciones
• Las soluciones no triviales existen cuando hay variables libres

Los sistemas se clasifican en:

• Sistema subdeterminado (m<n): tiene infinitas soluciones
• Sistema homogéneo: siempre tiene solución (al menos la trivial)
• Sistema sobredeterminado (m>n): puede no tener solución

La igualdad de matrices A=(aᵢⱼ) y B=(bᵢⱼ) requiere:

• Tener el mismo tamaño
• Que todos los elementos correspondientes sean iguales $aᵢⱼ=bᵢⱼ$

Operaciones matriciales básicas:

1. Suma de matrices: Se suman los elementos correspondientes $A+B$=$aᵢⱼ+bᵢⱼ$

   • Solo definida para matrices del mismo tamaño
   • Propiedades: A+0=A, A+B=B+A, $A+B$+C=A+$B+C$

2. Multiplicación por escalar: (αA)=(αaᵢⱼ)

   • Propiedades: 0·A=0, α$A+B$=αA+αB, (α+β)A=αA+βA

💡 Observación importante: En los sistemas homogéneos con más incógnitas que ecuaciones (m<n), siempre existen soluciones no triviales. Esto es fundamental para espacios vectoriales.

3. Producto matricial: (AB)ᵢⱼ = Σ aᵢₖbₖⱼ (suma del producto de elementos de la fila i de A por columna j de B)
   • Requiere que el número de columnas de A sea igual al número de filas de B

Propiedades de Operaciones Matriciales

El producto matricial tiene propiedades importantes:

• Asociatividad: (AB)C = A(BC)
• Distributividad: A$B+C$ = AB+AC y $A+B$C = AC+BC
• No conmutatividad: En general, AB ≠ BA
• Con la identidad: AI = IA = A

Una matriz identidad I tiene unos en la diagonal principal y ceros en el resto:

[1 0 0]
[0 1 0]
[0 0 1]

La suma de matrices $A+B$ está definida solo para matrices del mismo tamaño:

• A+B = $aᵢⱼ+bᵢⱼ$
• Propiedades: A+0=A, A+B=B+A, $A+B$+C=A+$B+C$

La multiplicación por escalar (αA) multiplica cada elemento de A por α:

• αA = $αaᵢⱼ$
• Propiedades: 1·A=A, (α+β)A=αA+βA, α$A+B$=αA+αB

💡 Recuerda: Al multiplicar matrices, el orden importa (AB≠BA). Además, el producto AB solo está definido si el número de columnas de A coincide con el número de filas de B.

Para resolver sistemas usando matrices $Ax=b$, si A es invertible, entonces x=A⁻¹b. Esto nos da directamente la solución única del sistema.

Producto Matricial y Propiedades

El producto matricial de A de tamaño m×n y B de tamaño n×p produce una matriz C de tamaño m×p donde:

• cᵢⱼ = (renglón i de A)·(columna j de B) = aᵢ₁b₁ⱼ + aᵢ₂b₂ⱼ + ... + aᵢₙbₙⱼ

Dos matrices son compatibles para multiplicación cuando el número de columnas de la primera coincide con el número de filas de la segunda.

Propiedades del producto matricial:

1. Asociativa: (AB)C = A(BC)
2. Distributiva:
   • A$B+C$ = AB+AC
   • $A+B$C = AC+BC
3. No conmutativa: En general, AB ≠ BA
4. Con la identidad: AI = IA = A
5. Con la matriz nula: A·0 = 0·A = 0

Propiedades de la suma:

• A+0 = A (0 es la matriz nula)
• 0·A = 0 (0 el escalar y 0 matriz nula)
• A+B = B+A (conmutativa)
• $A+B$+C = A+$B+C$ (asociativa)

💡 Visualización práctica: Puedes interpretar el producto AB como la aplicación de la transformación B seguida de la transformación A. Esto explica por qué el orden importa.

La representación matricial de un sistema Ax=b permite resolver muchos sistemas simultáneamente cambiando solo el vector b, manteniendo la misma matriz de coeficientes A.

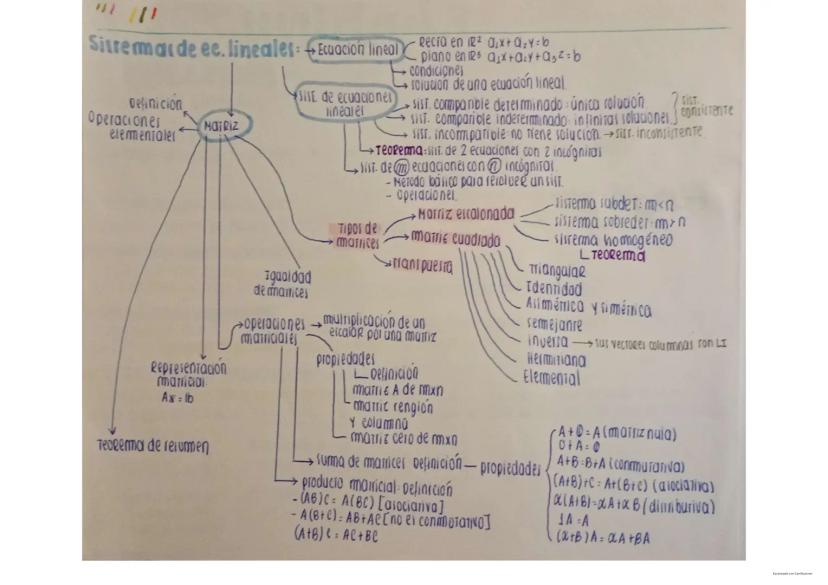
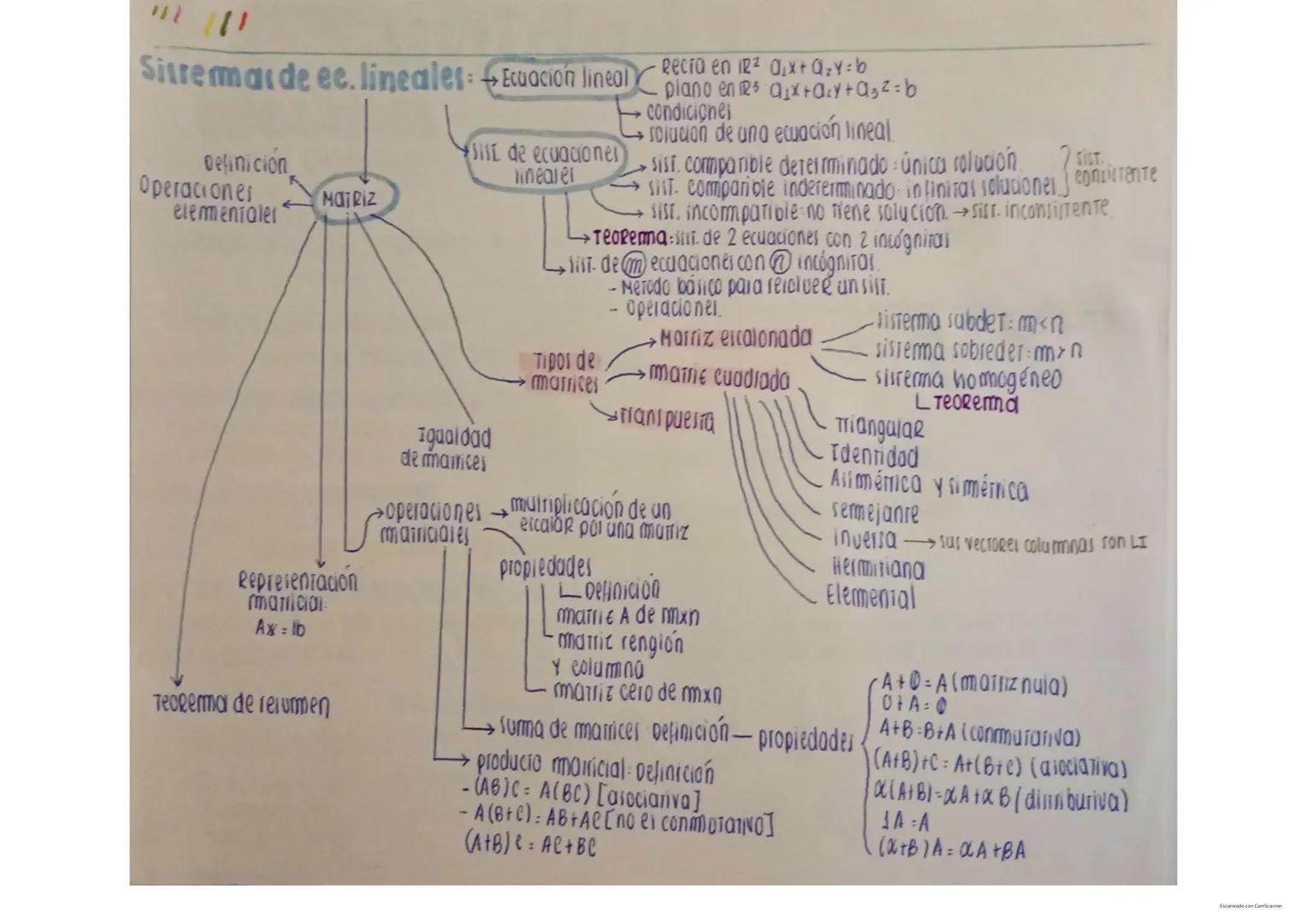
Matrices y Sistemas Homogéneos

Un sistema homogéneo tiene la forma Ax=0, donde todas las constantes independientes son cero. Estos sistemas siempre tienen al menos la solución trivial $x=0$.

Teorema importante: Un sistema homogéneo de m ecuaciones con n incógnitas tiene infinitas soluciones si m<n (menos ecuaciones que incógnitas).

Propiedades de sistemas no homogéneos:

• Si x₁ y x₂ son soluciones de Ax=b, entonces su diferencia x₁-x₂ es solución del sistema homogéneo asociado Ax=0
• Si x es una solución particular de Ax=b y h es solución de Ax=0, entonces x+h también es solución de Ax=b

Para encontrar todas las soluciones de un sistema no homogéneo Ax=b:

1. Encontrar una solución particular xₚ de Ax=b
2. Encontrar todas las soluciones xₕ del sistema homogéneo Ax=0
3. La solución general será y = xₚ + xₕ

Para sistemas compatibles indeterminados, la solución se expresa en términos de parámetros:

x = xₚ + t·v₁ + s·v₂ + ...

Donde t, s, ... son parámetros libres y v₁, v₂, ... son vectores del espacio nulo.

💡 Consejo práctico: Para resolver un sistema, trabaja primero con la matriz aumentada. Si quieres todas las soluciones de un sistema no homogéneo, busca primero una solución particular y luego las soluciones del sistema homogéneo asociado.

Matriz Inversa e Identidad

La matriz identidad I es una matriz cuadrada con unos en la diagonal principal y ceros en el resto. Tiene propiedades especiales:

• Para cualquier matriz A de tamaño adecuado: AI = IA = A

La matriz inversa A⁻¹ de una matriz cuadrada A cumple:

• A·A⁻¹ = A⁻¹·A = I
• No todas las matrices cuadradas tienen inversa
• Una matriz sin inversa se llama singular

Teoremas importantes:

1. Si una matriz es invertible, su inversa es única
2. Si A y B son invertibles, entonces AB también es invertible y (AB)⁻¹ = B⁻¹A⁻¹
3. Si A es invertible, entonces Aⁿ es invertible y (Aⁿ)⁻¹ = (A⁻¹)ⁿ
4. Si A es invertible y k≠0, entonces kA es invertible y (kA)⁻¹ = $1/k$A⁻¹

Para calcular la matriz inversa:

1. Formar la matriz aumentada $A|I$
2. Aplicar operaciones elementales para transformar A en I
3. La parte derecha se transformará en A⁻¹

Si A es invertible, el sistema Ax=b tiene solución única x=A⁻¹b.

💡 Aplicación importante: La matriz inversa nos permite resolver sistemas de ecuaciones de forma directa. Si A es invertible, la solución de Ax=b es simplemente x=A⁻¹b.

Las demostraciones de propiedades matriciales utilizan definiciones básicas y operaciones algebraicas para establecer resultados fundamentales del álgebra lineal.

Propiedades Adicionales de Matrices

Las demostraciones de propiedades matriciales utilizan operaciones algebraicas básicas:

Propiedad: 1A = A Demostración: 1A = $1·a₁₁ 1·a₁₂ ... 1·a₁ₙ$ $1·a₂₁ 1·a₂₂ ... 1·a₂ₙ$ $... ... ... ...$ $1·aₘ₁ 1·aₘ₂ ... 1·aₘₙ$ = A

Propiedad: (α+β)A = αA + βA Demostración: (α+β)A = $(α+β)a₁₁ (α+β)a₁₂ ... (α+β)a₁ₙ$ $(α+β)a₂₁ (α+β)a₂₂ ... (α+β)a₂ₙ$ $... ... ... ...$ $(α+β)aₘ₁ (α+β)aₘ₂ ... (α+β)aₘₙ$

Por la propiedad distributiva de los reales: (α+β)aᵢⱼ = αaᵢⱼ + βaᵢⱼ

Por tanto: (α+β)A = $αa₁₁+βa₁₁ αa₁₂+βa₁₂ ... αa₁ₙ+βa₁ₙ$ $αa₂₁+βa₂₁ αa₂₂+βa₂₂ ... αa₂ₙ+βa₂ₙ$ $... ... ... ...$ $αaₘ₁+βaₘ₁ αaₘ₂+βaₘ₂ ... αaₘₙ+βaₘₙ$ = αA + βA

💡 Nota práctica: Estas propiedades son fundamentales para manipular expresiones con matrices y resolver sistemas complejos. Dominando estas propiedades, podrás simplificar operaciones matriciales complejas.

Las matrices nos proporcionan una notación compacta y potente para representar transformaciones y sistemas de ecuaciones.

Sistemas Homogéneos y Teoremas Importantes

Los sistemas homogéneos $Ax=0$ tienen propiedades especiales:

1. Siempre tienen la solución trivial x=0
2. Si tienen más incógnitas que ecuaciones (m<n), garantizan infinitas soluciones

Teorema fundamental: Si x₁ y x₂ son soluciones de un sistema no homogéneo Ax=b, entonces su diferencia x₁-x₂ es solución del sistema homogéneo asociado Ax=0.

Demostración:

• Si x₁ es solución de Ax=b → Ax₁=b
• Si x₂ es solución de Ax=b → Ax₂=b
• Restando: A$x₁-x₂$ = Ax₁-Ax₂ = b-b = 0
• Por lo tanto, x₁-x₂ es solución de Ax=0

Corolario: Sea x una solución particular de Ax=b y h una solución del sistema homogéneo Ax=0, entonces y=x+h también es solución de Ax=b.

Aplicación práctica: Para encontrar todas las soluciones de un sistema no homogéneo:

1. Encontrar una solución particular xₚ
2. Encontrar todas las soluciones del sistema homogéneo asociado xₕ
3. La solución general es y = xₚ + t·xₕ (donde t es un parámetro)

Ejemplo: Para el sistema: x₁-x₂+x₃=6 5x₁-5x₂+3x₃=18

La solución general es: y = $6, 0, 0$ + t$-5, 0, 1$

💡 Estrategia clave: Al resolver sistemas con infinitas soluciones, identifica primero una solución particular sencilla (asignando valores a las variables libres). Luego, encuentra las soluciones del sistema homogéneo para obtener los vectores de dirección.