Fundamentos de la Función Cuadrática

La función cuadrática tiene una expresión general que se conoce como forma polinómica:

y = ax² + bx + c

Donde "a" es el coeficiente principal (nunca puede ser cero), "b" es el coeficiente del término lineal y "c" es el término independiente. El dominio de estas funciones abarca todos los números reales $Dₑ = ℝ$.

Al graficar una función cuadrática obtenemos una parábola, una curva simétrica respecto a una recta vertical llamada eje de simetría. Para trazar correctamente la parábola necesitamos identificar elementos clave como el vértice, los puntos de corte con los ejes y las ramas.

💡 Piensa en la parábola como una "U" que puede estar orientada hacia arriba o abajo. Los elementos como vértice y raíces están directamente relacionados con los coeficientes a, b y c.

Concavidad y Forma de la Parábola

La concavidad define la orientación de la parábola y está determinada por el signo del coeficiente principal:

• Si a > 0: las ramas de la parábola se abren hacia arriba (forma de "U")
• Si a < 0: las ramas se abren hacia abajo (forma de "U" invertida)

El valor absoluto de "a" influye en qué tan abierta o cerrada es la parábola. Cuanto mayor es |a|, más "cerradas" o "contraídas" están sus ramas (parábola más angosta).

Por ejemplo, si comparamos y = 0,5x², y = x², y = 2x² y y = 5x², todas tienen concavidad hacia arriba, pero la parábola se vuelve más estrecha a medida que el coeficiente "a" aumenta.

🔍 Observá cómo cambia la "apertura" de la parábola: las funciones con coeficientes como 0,5 son muy abiertas, mientras que las que tienen coeficientes como 5 son mucho más cerradas.

Intersección con el Eje Y

El punto de corte con el eje Y es uno de los elementos más fáciles de encontrar en una función cuadrática. Está determinado directamente por el término independiente (c).

Cuando evaluamos la función en x = 0, obtenemos: y = f(0) = a·0² + b·0 + c = c

Esto significa que la parábola siempre corta el eje Y en el punto (0, c). Por ejemplo:

• Si c = 3, la parábola corta el eje Y en el punto (0, 3)
• Si c = 0, la parábola pasa por el origen
• Si c = -2, la parábola corta el eje Y en (0, -2)

Este punto de corte es independiente de los valores de "a" y "b", lo que lo convierte en una referencia rápida para comenzar a graficar cualquier función cuadrática.

🧠 Para recordar fácilmente: el valor de c siempre te indica la "altura" a la que la parábola cruza el eje Y.

Raíces y Forma Factorizada

Las raíces de una función cuadrática son los valores de x donde la función vale cero, es decir, los puntos donde la parábola corta el eje X. Para encontrarlas, igualamos la función a cero y resolvemos la ecuación cuadrática:

ax² + bx + c = 0

La fórmula de Bhaskara nos da las soluciones: r₁,₂ = $-b ± √(b² - 4ac)$/2a

La expresión bajo el radical, Δ = b² - 4ac, se llama discriminante y determina cuántas raíces tendrá la función:

• Si Δ < 0: la función no tiene raíces reales (la parábola no corta el eje X)
• Si Δ > 0: la función tiene dos raíces reales distintas (la parábola corta el eje X en dos puntos)
• Si Δ = 0: la función tiene una raíz real doble (la parábola toca el eje X en un solo punto)

⚡ Cuando logras factorizar una función cuadrática en la forma f(x) = a$x-r₁$$x-r₂$, puedes identificar inmediatamente las raíces r₁ y r₂. Esta es la llamada forma factorizada de la función.

Formas de Expresar una Función Cuadrática

Conociendo las raíces de una función polinómica, podemos escribirla en su forma factorizada: f(x) = a$x-r₁$$x-r₂$

Donde r₁ y r₂ son las raíces. Si la función tiene una única raíz doble, la expresión será: f(x) = a$x-r$²

El vértice es el punto donde la parábola cambia de dirección y por donde pasa el eje de simetría. Dependiendo de la concavidad:

• Si a > 0: el vértice es un punto mínimo
• Si a < 0: el vértice es un punto máximo

Las coordenadas del vértice se pueden calcular a partir de los coeficientes:

• Coordenada x: h = -b/(2a)
• Coordenada y: k = -Δ/(4a) = -$b²-4ac$/(4a)

El eje de simetría es la recta vertical que pasa por la coordenada x del vértice: x = -b/(2a)

🌟 El vértice es quizás el punto más importante de una parábola. Representa el valor mínimo o máximo que alcanza la función, dependiendo de su concavidad.

El Eje de Simetría y la Forma Canónica

El eje de simetría es la recta vertical que pasa por el vértice y divide a la parábola en dos partes idénticas. Su ecuación es:

x = -b/(2a)

Esta línea es fundamental porque nos permite:

• Encontrar puntos simétricos en la parábola
• Localizar el vértice sobre el eje
• Comprender la relación entre las raíces

Las coordenadas del vértice V(h,k) también se pueden escribir como: V$-b/(2a), -Δ/(4a)$

Existe una tercera forma de escribir la función cuadrática, llamada forma canónica: y = a$x-h$² + k

Esta expresión es muy útil porque muestra directamente:

• Las coordenadas del vértice (h,k)
• La concavidad (signo de a)
• El "desplazamiento" de la parábola respecto a la función básica y = ax²

💯 La forma canónica es la mejor expresión para visualizar rápidamente cómo se ve la parábola, ya que contiene explícitamente la información del vértice y la concavidad.

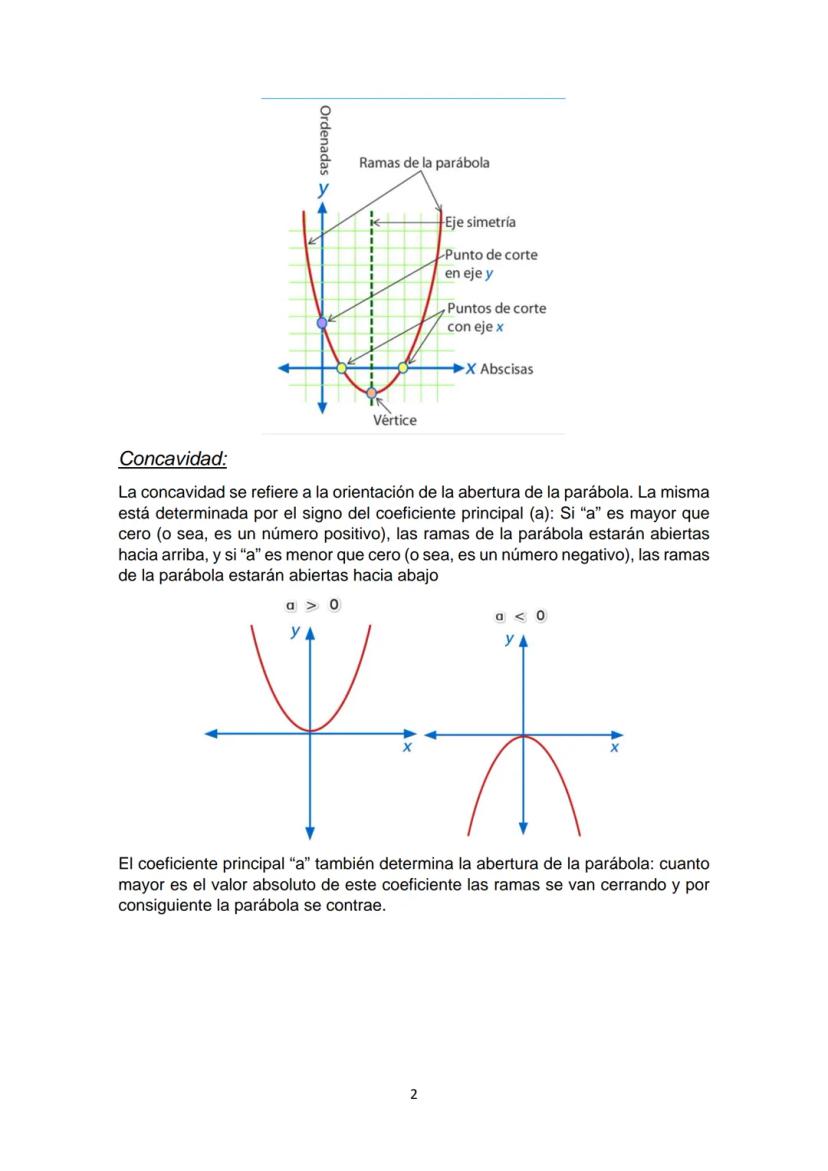
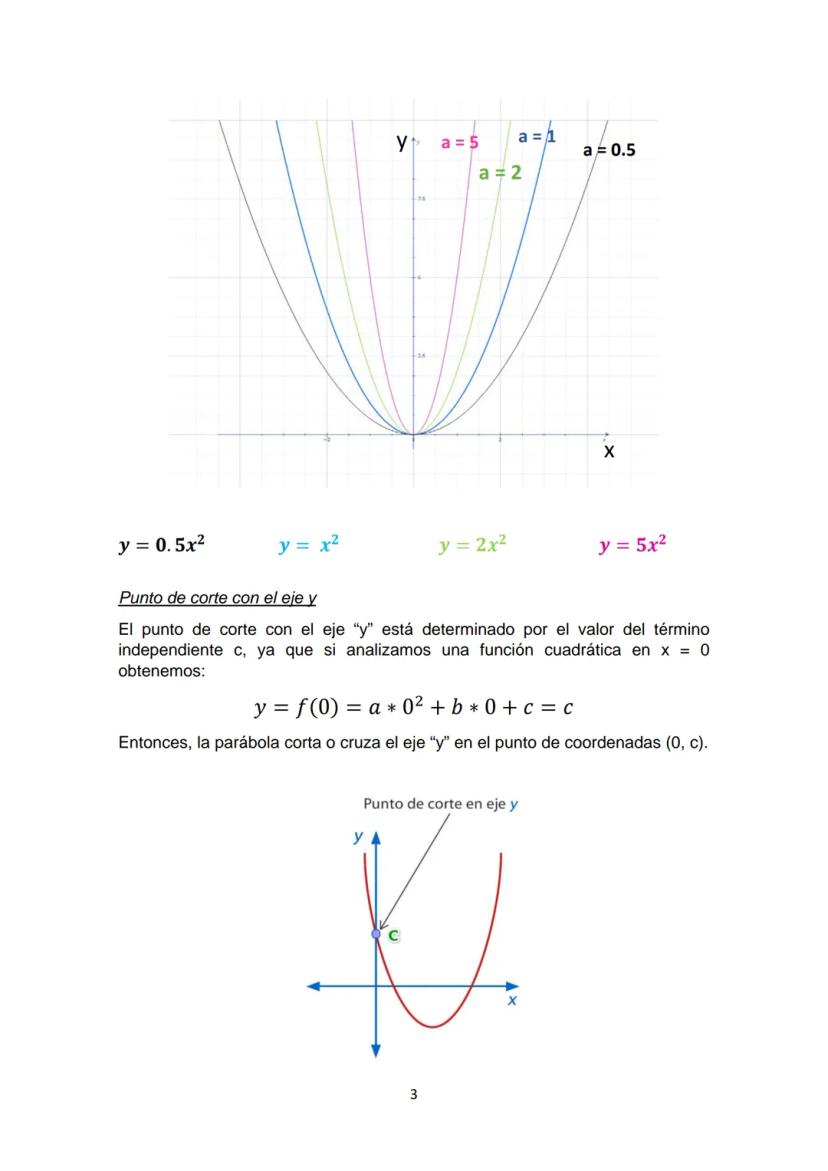
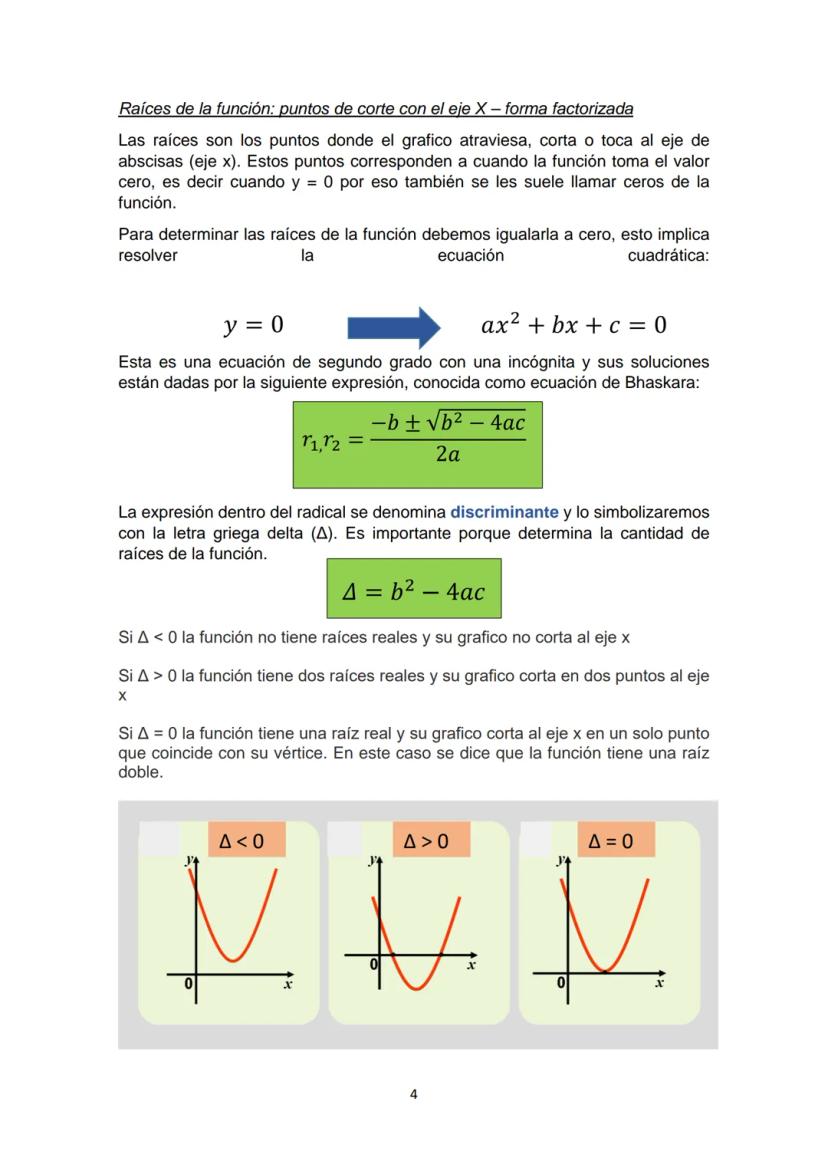
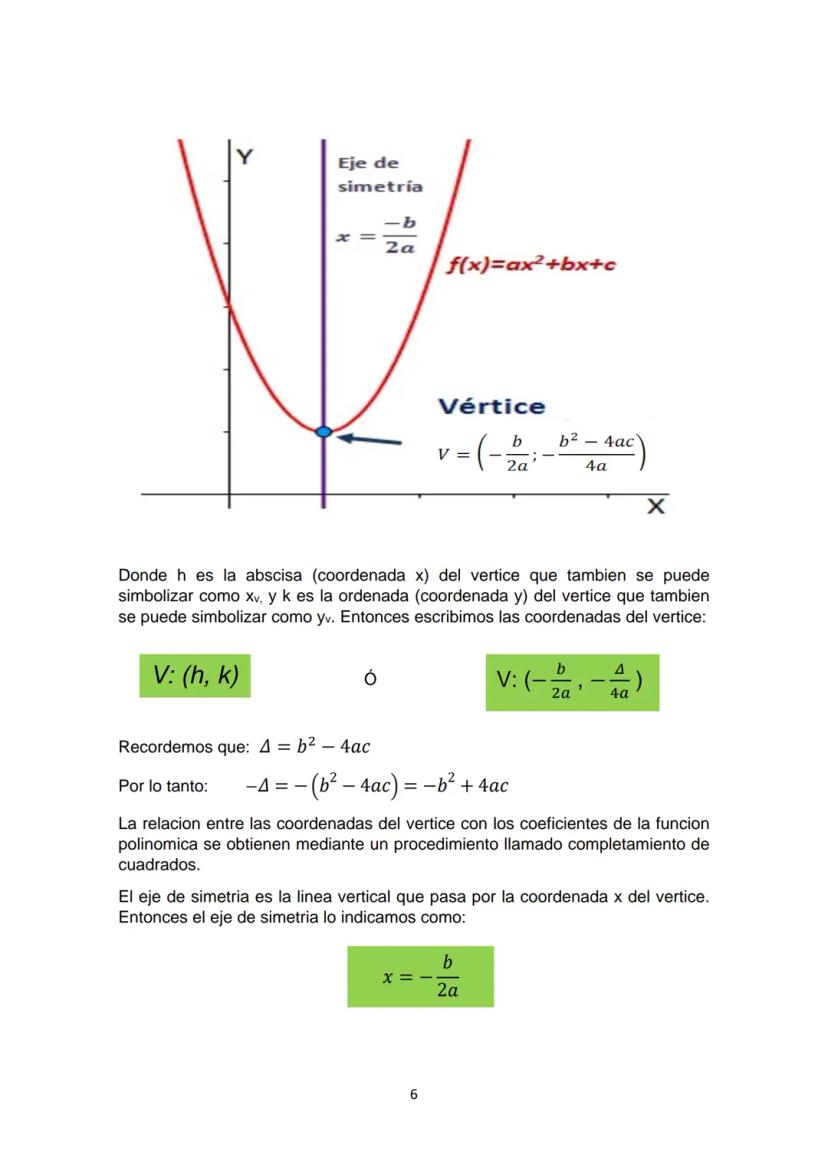
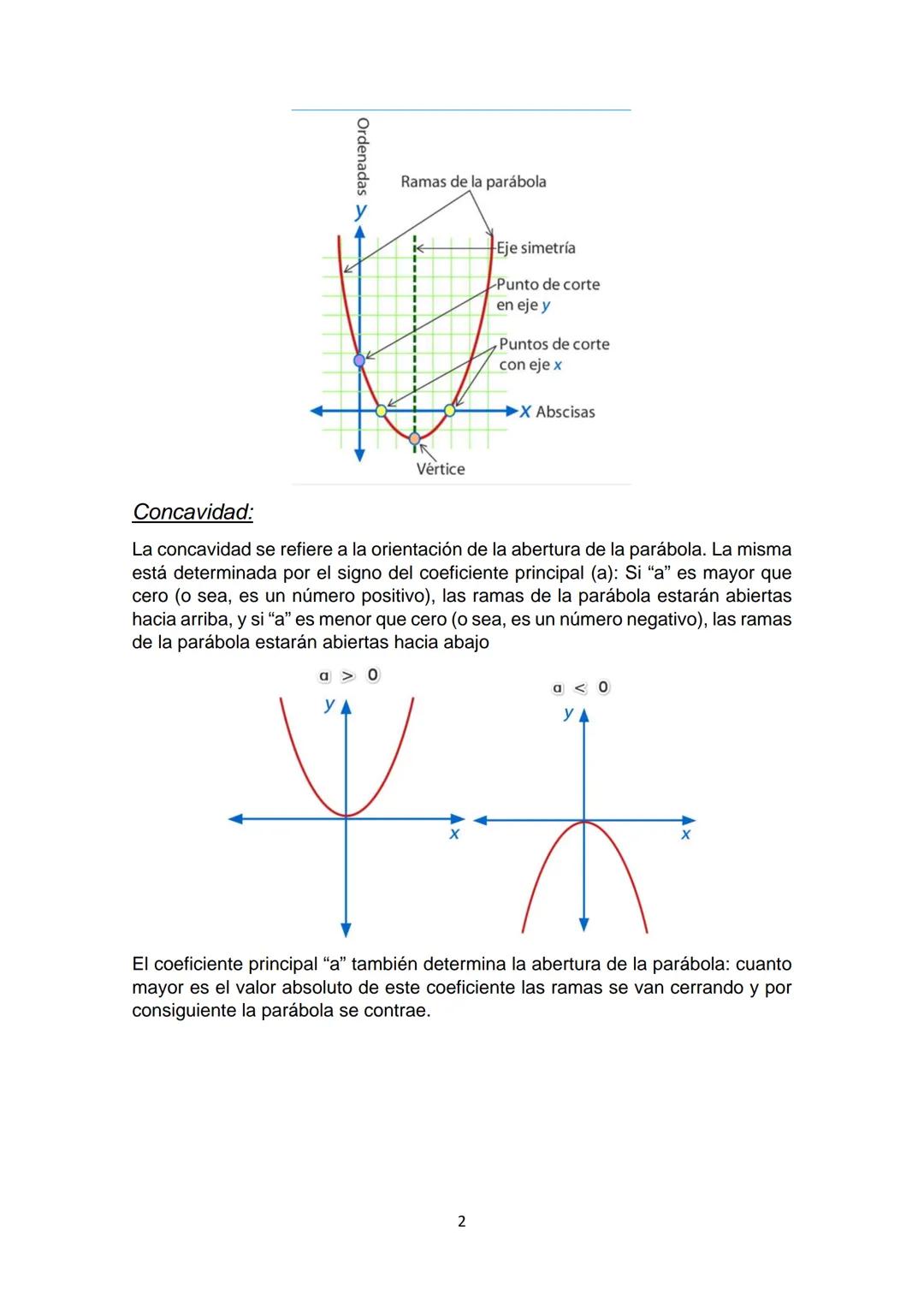
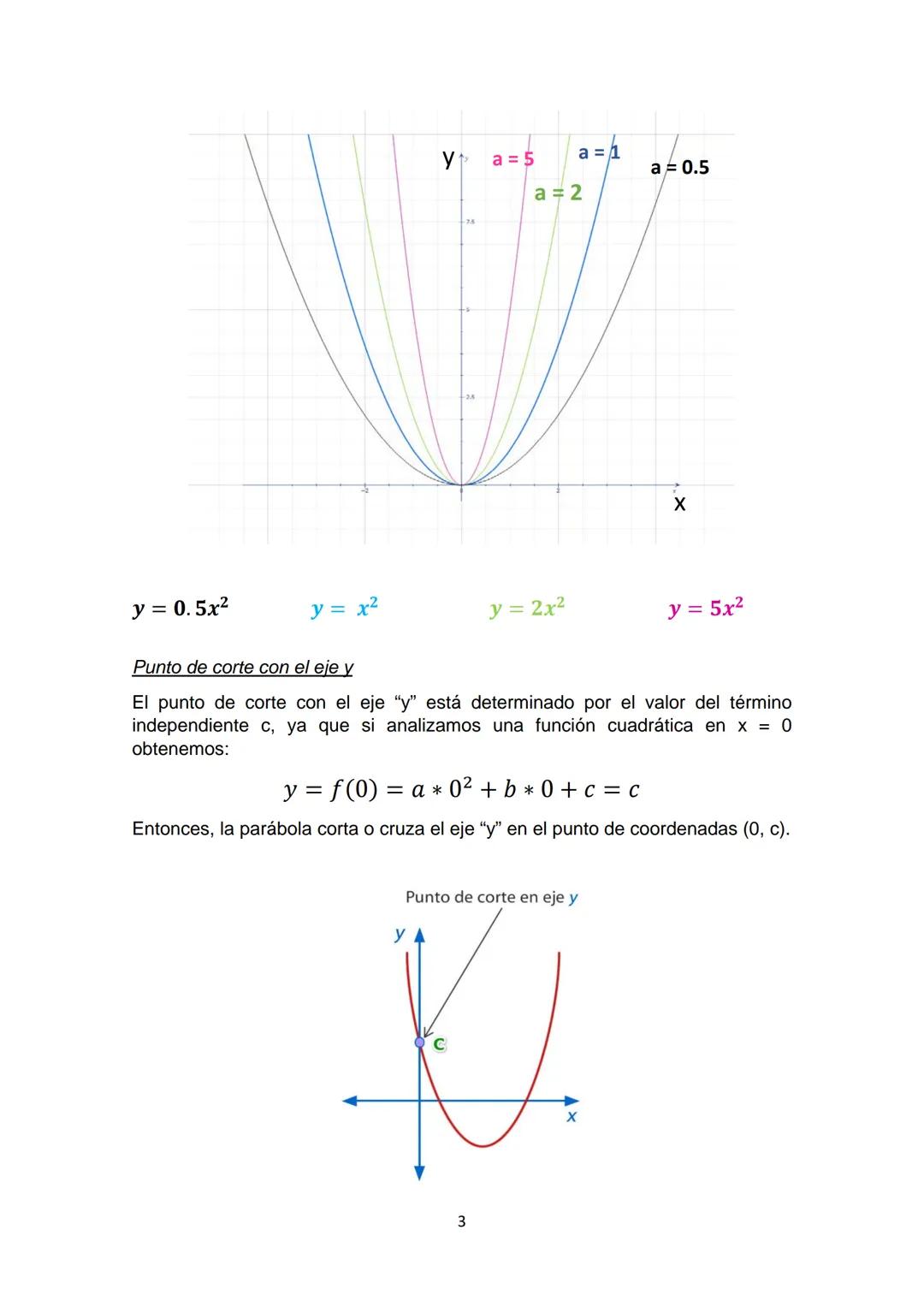
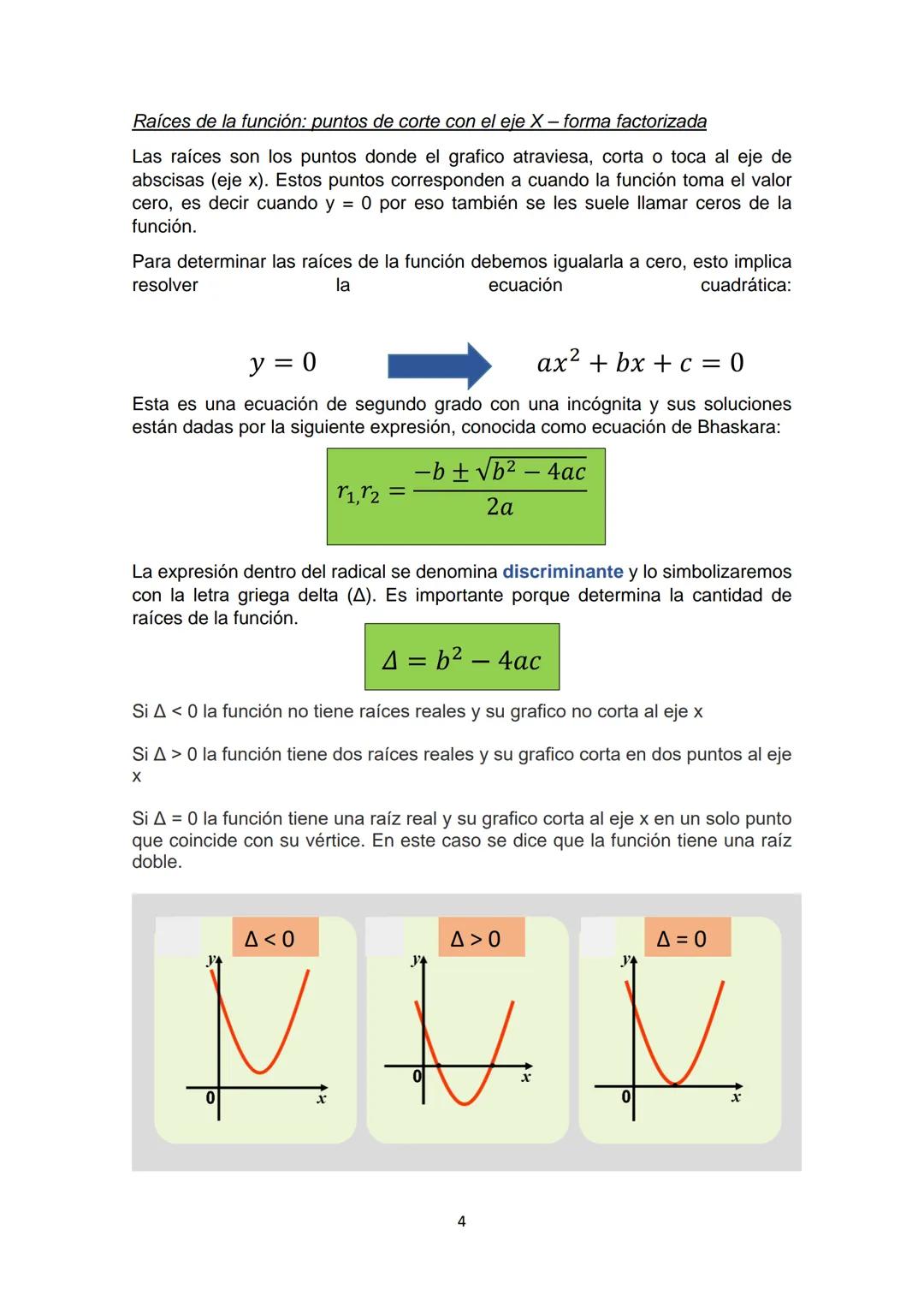
Relación Entre Vértice y Raíces

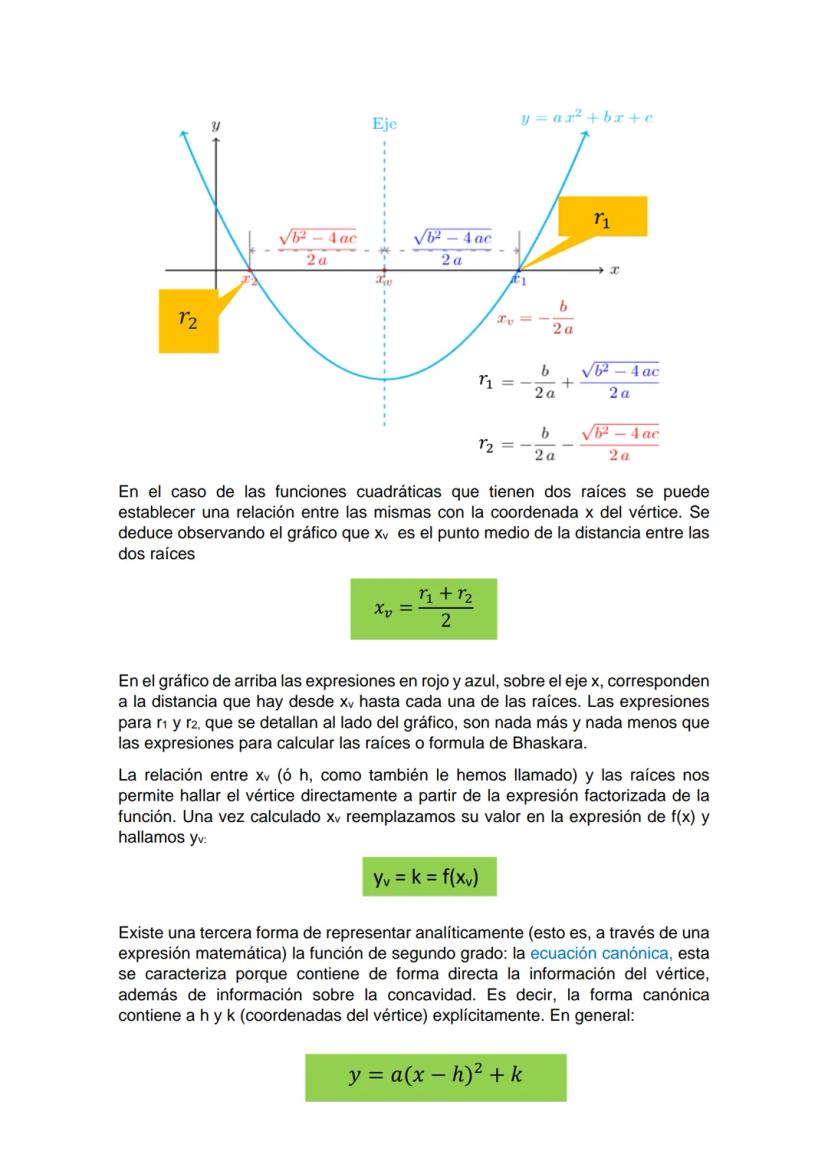
En las funciones cuadráticas con dos raíces, existe una relación importante entre la coordenada x del vértice (xᵥ) y las raíces r₁ y r₂:

xᵥ = $r₁ + r₂$/2

Esto significa que la coordenada x del vértice es el punto medio entre las dos raíces. Esta propiedad nos permite:

• Encontrar el vértice si conocemos las raíces
• Verificar nuestros cálculos
• Entender mejor la simetría de la parábola

Para hallar la coordenada y del vértice, simplemente evaluamos la función en xᵥ: yᵥ = f(xᵥ)

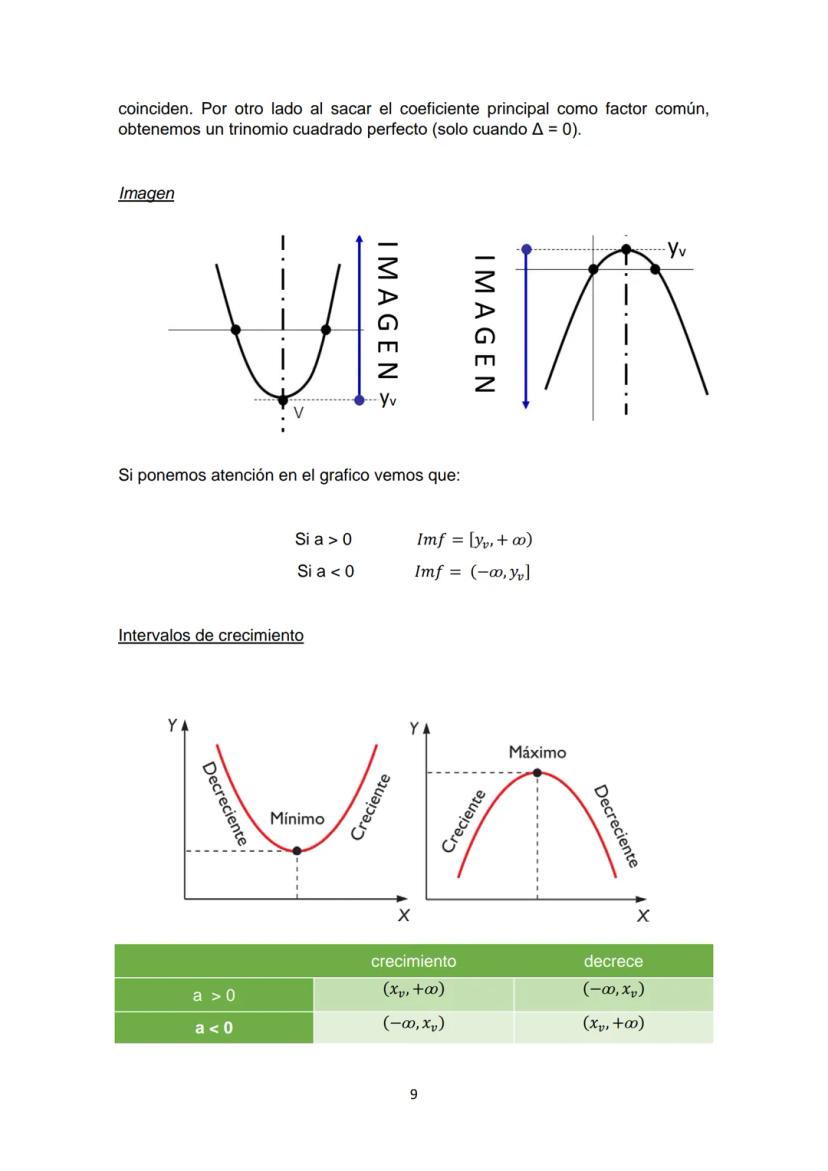
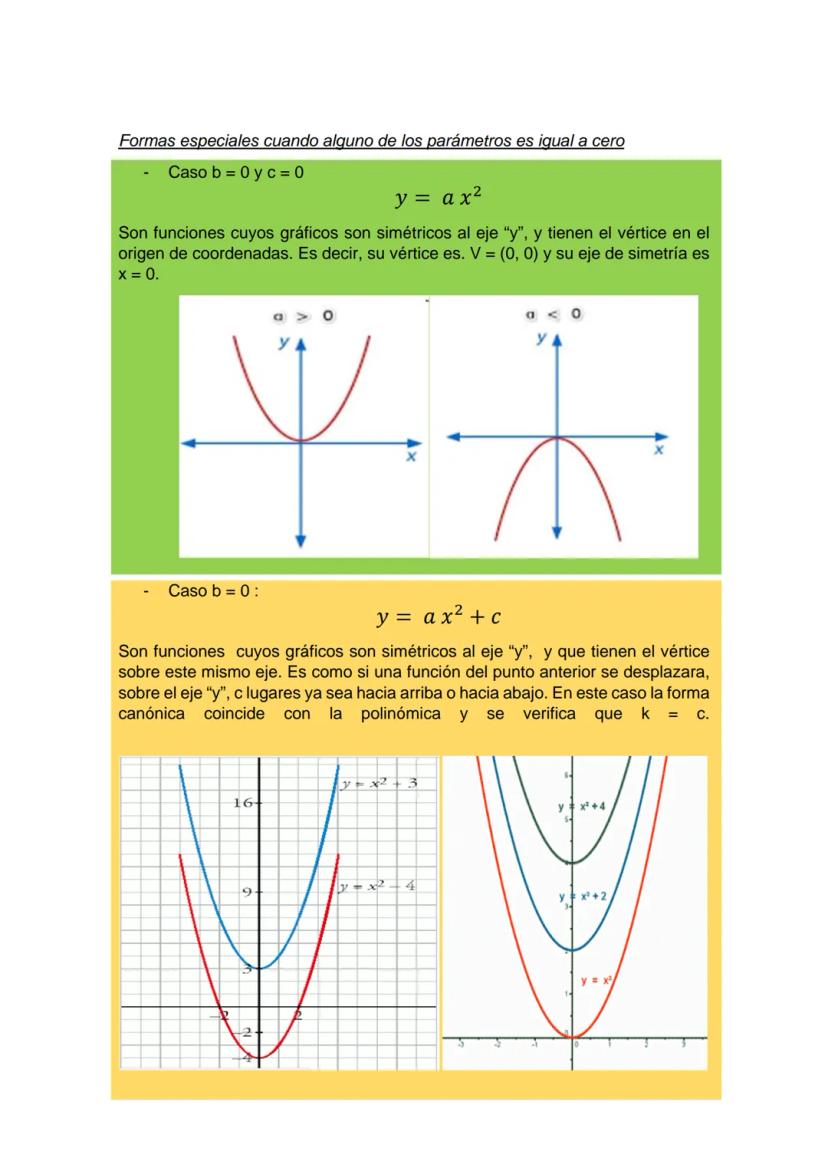
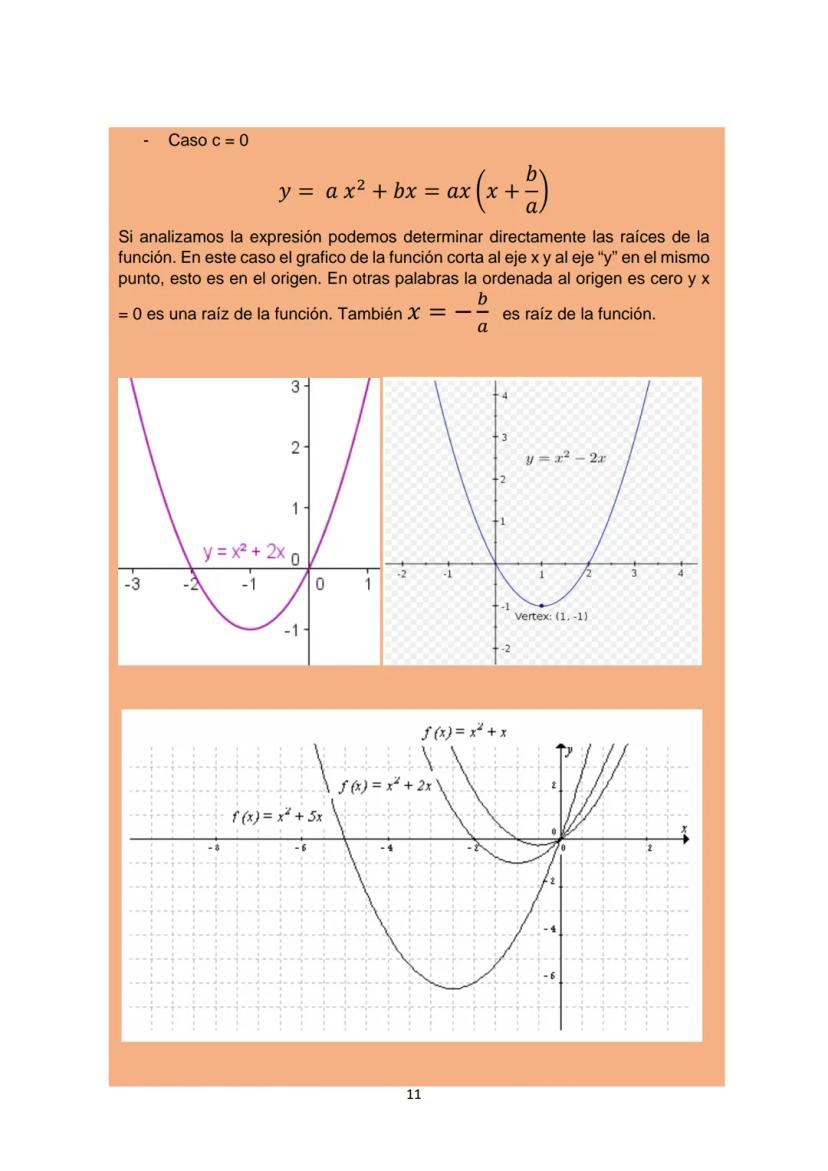
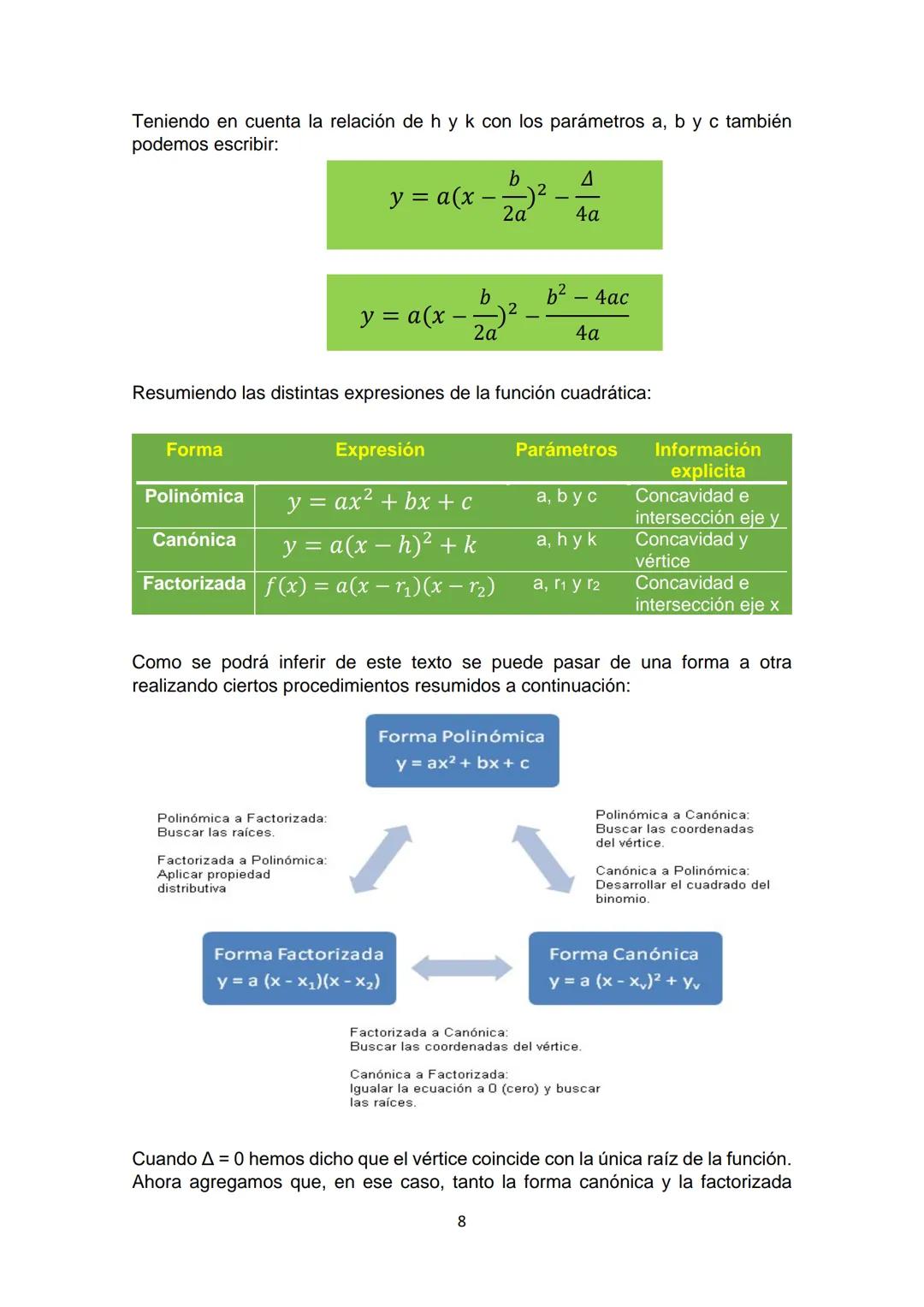
La forma canónica de la función cuadrática es: y = a$x-h$² + k

Donde (h,k) son las coordenadas del vértice. Esta forma también se puede escribir como: y = a$x-b/(2a)$² - Δ/(4a)

🔄 Podemos convertir entre las tres formas de la función cuadrática (polinómica, canónica y factorizada) según lo que necesitemos analizar: intersecciones con los ejes, vértice o raíces.

Las Tres Formas de la Función Cuadrática

Cada representación de la función cuadrática nos da información diferente:

1. Forma Polinómica: y = ax² + bx + c

   • Muestra directamente la concavidad (a) y la intersección con eje Y (c)
   • Es la forma más común de presentar la función

2. Forma Canónica: y = a$x-h$² + k

   • Muestra directamente el vértice (h,k) y la concavidad (a)
   • Ideal para estudiar máximos, mínimos y simetría

3. Forma Factorizada: y = a$x-r₁$$x-r₂$

   • Muestra directamente las raíces (r₁ y r₂) y la concavidad (a)
   • Ideal para estudiar intersecciones con el eje X

Podemos convertir entre estas formas mediante procedimientos específicos:

• De Polinómica a Factorizada: encontramos las raíces
• De Factorizada a Polinómica: aplicamos propiedad distributiva
• De Polinómica a Canónica: encontramos el vértice
• De Canónica a Polinómica: desarrollamos el cuadrado del binomio

🔍 Cuando el discriminante es cero (Δ = 0), la forma canónica y la factorizada tienen estructuras muy similares, ya que el vértice coincide con la única raíz de la función.

Imagen e Intervalos de Crecimiento

La imagen de la función cuadrática (el rango de valores de y que puede tomar) depende de la concavidad y del vértice:

• Si a > 0: Im(f) = [yᵥ, +∞) → La función tiene un mínimo en el vértice
• Si a < 0: Im(f) = (-∞, yᵥ] → La función tiene un máximo en el vértice

Los intervalos de crecimiento y decrecimiento también dependen de la concavidad:

Para a > 0:

• La función decrece en $-∞, xᵥ$
• La función crece en $xᵥ, +∞$

Para a < 0:

• La función crece en $-∞, xᵥ$
• La función decrece en $xᵥ, +∞$

Esto significa que la función siempre cambia de dirección exactamente en el vértice, lo que refuerza la importancia de este punto en el análisis de funciones cuadráticas.

📈 Un truco para recordar: en las parábolas con forma de "U" (a > 0), la función siempre decrece hasta llegar al vértice y luego comienza a crecer.

Casos Especiales de Funciones Cuadráticas

Cuando algunos coeficientes son cero, obtenemos formas particulares:

Cuando b = 0 y c = 0: y = ax²

• El vértice está en el origen (0,0)
• La parábola es simétrica respecto al eje Y
• El eje de simetría es x = 0

Cuando solo b = 0: y = ax² + c

• El vértice está sobre el eje Y en (0,c)
• La parábola es simétrica respecto al eje Y
• La forma canónica coincide con la polinómica
• Es como si desplazáramos verticalmente la parábola y = ax²

Estas funciones son especialmente sencillas de graficar porque mantienen su simetría respecto al eje Y, lo que nos permite trazar la parábola con mayor facilidad.

🎯 Las funciones de la forma y = ax² + c son perfectas para practicar el concepto de traslación vertical de funciones: el término "c" desplaza la parábola hacia arriba (si c > 0) o hacia abajo (si c < 0).