Cónicas: Introducción y Clasificación

Las cónicas son curvas que resultan de la intersección entre un cono recto y planos en diferentes ángulos. Dependiendo de la posición del plano, obtenemos distintas figuras: parábolas, elipses e hipérbolas.

Todas las cónicas comparten una propiedad llamada excentricidad, que se define como el cociente entre la distancia de un punto de la curva al foco y la distancia de ese mismo punto a una recta llamada directriz. Esta excentricidad (e) nos permite clasificarlas:

• Si e = 1: parábola
• Si e < 1: elipse
• Si e > 1: hipérbola

La ecuación general de una cónica es $Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0$. Cuando B = 0 (cónica no rotada), podemos identificar el tipo de cónica analizando los coeficientes:

• Si A y C tienen signos opuestos: hipérbola
• Si A y C tienen el mismo signo: elipse
• Si uno de ellos es cero: parábola

💡 Puedes recordar fácilmente cómo identificar cada cónica: cuando un plano es paralelo a una generatriz del cono, forma una parábola; cuando es paralelo a dos generatrices, forma una hipérbola; y cuando no es paralelo a ninguna generatriz, forma una elipse.

Geometría y Cónicas: Elementos Fundamentales

La excentricidad constituye el eje central en el estudio de las cónicas. Esta medida nos permite entender cómo se comportan estas curvas y predecir sus formas.

La circunferencia es un caso especial de elipse donde sus dos focos coinciden. Su ecuación estándar es $(x - h)^2 + (y - k)^2 = r^2$, donde $(h, k)$ es el centro y $r$ es el radio. En su forma general aparece como $x^2 + y^2 + Dx + Ey + F = 0$.

Para representarla paramétricamente usamos:

• $x = x_0 + r \cos\theta$
• $y = y_0 + r \sin\theta$

La parábola se define como el lugar geométrico de puntos que equidistan de un punto fijo (foco) y una recta fija (directriz). Sus elementos clave incluyen:

• Vértice: punto donde la parábola cambia de dirección
• Eje de simetría: línea que divide la parábola en partes simétricas
• Foco: punto que se encuentra a una distancia $p$ del vértice
• Lado recto: cuerda perpendicular al eje de simetría que pasa por el foco, con longitud $|4p|$

📝 Una propiedad fascinante de la parábola es su capacidad de concentrar rayos paralelos en su foco, principio utilizado en antenas parabólicas y faros de automóviles. ¡La matemática en acción!

Hipérbola: Características y Ecuaciones

La hipérbola es el lugar geométrico donde la diferencia de distancias de cualquier punto a dos puntos fijos (focos) es constante. Su ecuación canónica, cuando está centrada en el origen, es $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$.

Características principales:

• Centro: punto medio entre los focos
• Dos focos y dos vértices
• Semieje real ($a$): distancia del centro al vértice
• Semieje imaginario ($b$): relacionado con la apertura de las ramas
• Relación fundamental: $c^2 = a^2 + b^2$, donde $c$ es la distancia del centro al foco

Las asíntotas son rectas que la hipérbola se aproxima infinitamente sin tocarlas nunca. Para una hipérbola horizontal, se expresan como $y = \pm \frac{b}{a}x$.

Cuando el centro de la hipérbola se desplaza a $(h,k)$, su ecuación se convierte en $\frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2} = 1$. Para una hipérbola vertical, los términos del numerador se intercambian.

💡 Para recordar fácilmente las ecuaciones de las asíntotas: dibuja un rectángulo con lados de longitud $2a$ y $2b$ centrado en el origen. Las diagonales extendidas de este rectángulo son precisamente las asíntotas.

Geometría Analítica: Segmentos y Distancias

La geometría analítica nos permite trabajar con elementos geométricos utilizando coordenadas y ecuaciones. Un concepto fundamental es el segmento dirigido, que tiene tanto longitud como dirección.

La distancia entre dos puntos $P_1(x_1,y_1)$ y $P_2(x_2,y_2)$ se calcula mediante el teorema de Pitágoras:

$d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Para dividir un segmento en una razón dada $r$, podemos usar las fórmulas:

$x = \frac{x_1+rx_2}{1+r}$ y $y = \frac{y_1+ry_2}{1+r}$

Estas fórmulas nos permiten encontrar las coordenadas de un punto $P(x,y)$ que divide el segmento $P_1P_2$ en la razón $r$.

Características importantes sobre la razón $r$:

• Si $P$ está en el segmento $P_1P_2$, entonces $r > 0$
• Si $P$ coincide con $P_1$, entonces $r = 0$
• Si $P$ está fuera del segmento, entonces $r < 0$

💡 El punto medio es un caso especial donde $r = 1$, lo que nos da las conocidas fórmulas $x = \frac{x_1+x_2}{2}$ y $y = \frac{y_1+y_2}{2}$. ¡Es más fácil de recordar si piensas en promediar las coordenadas!

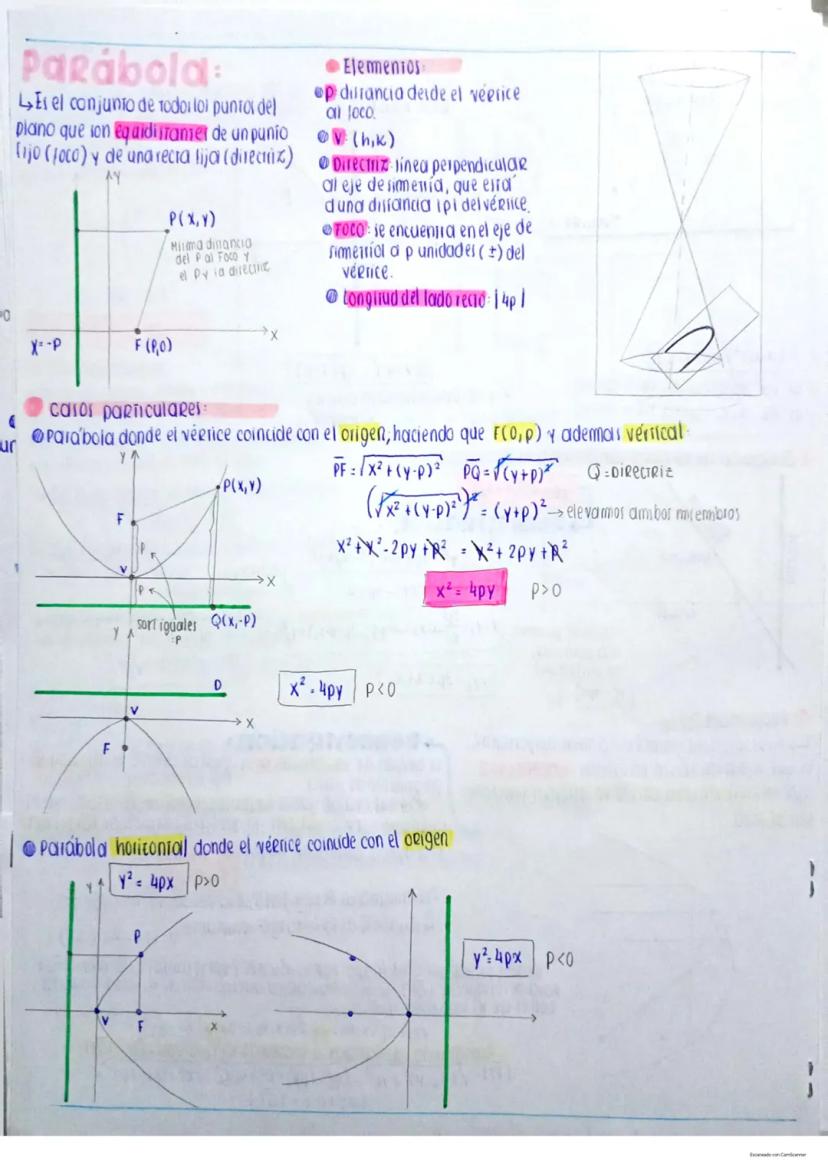
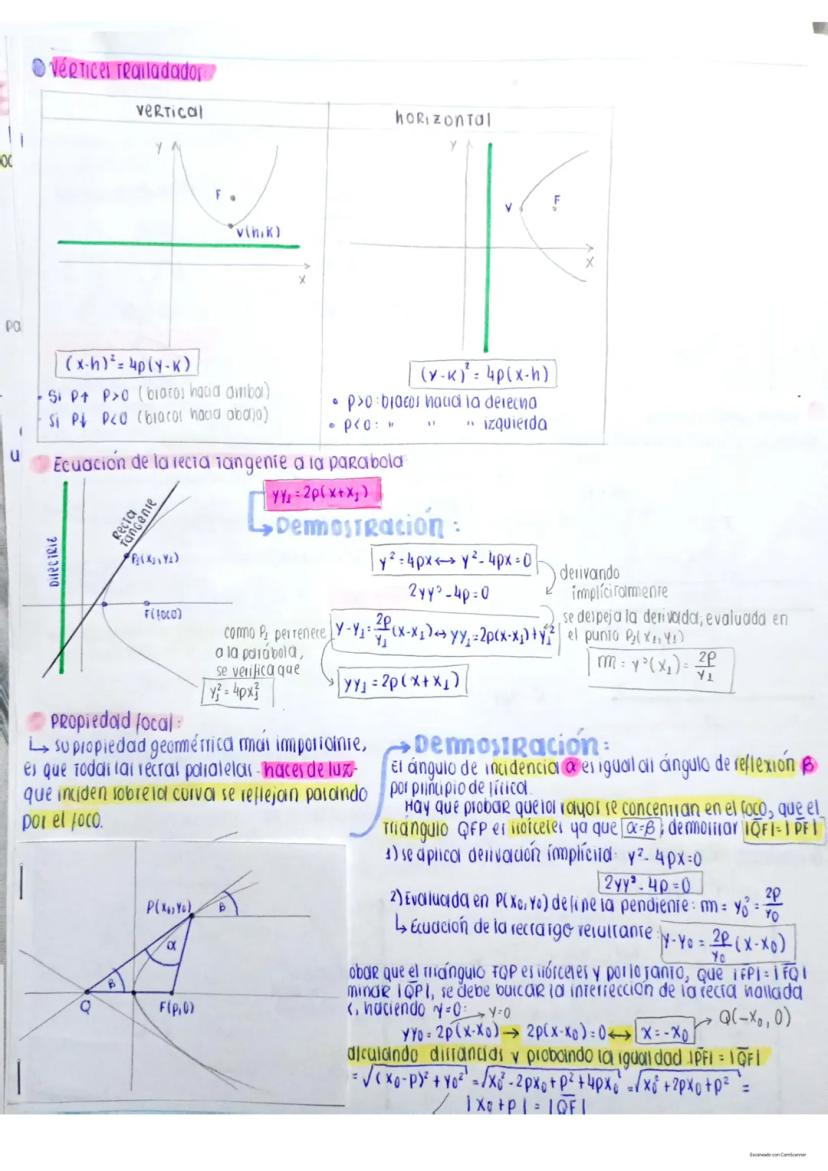
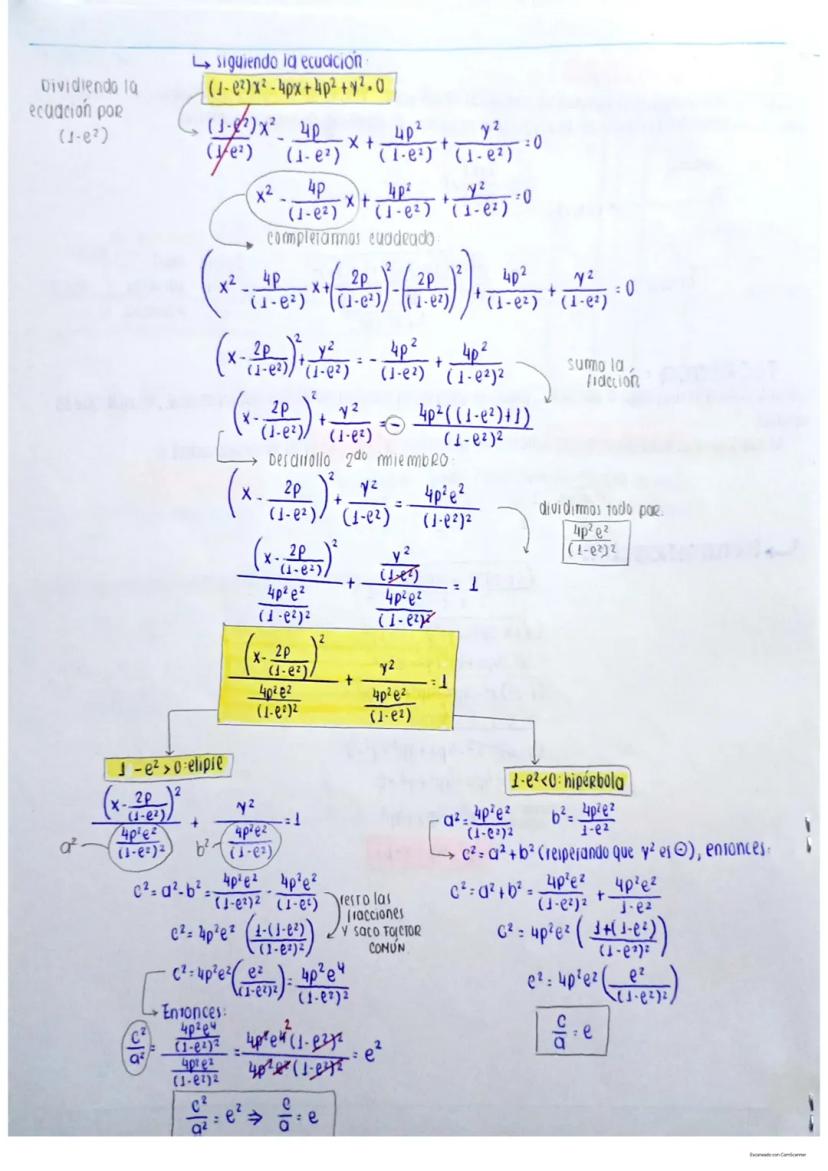
Circunferencia: Definición y Ecuaciones

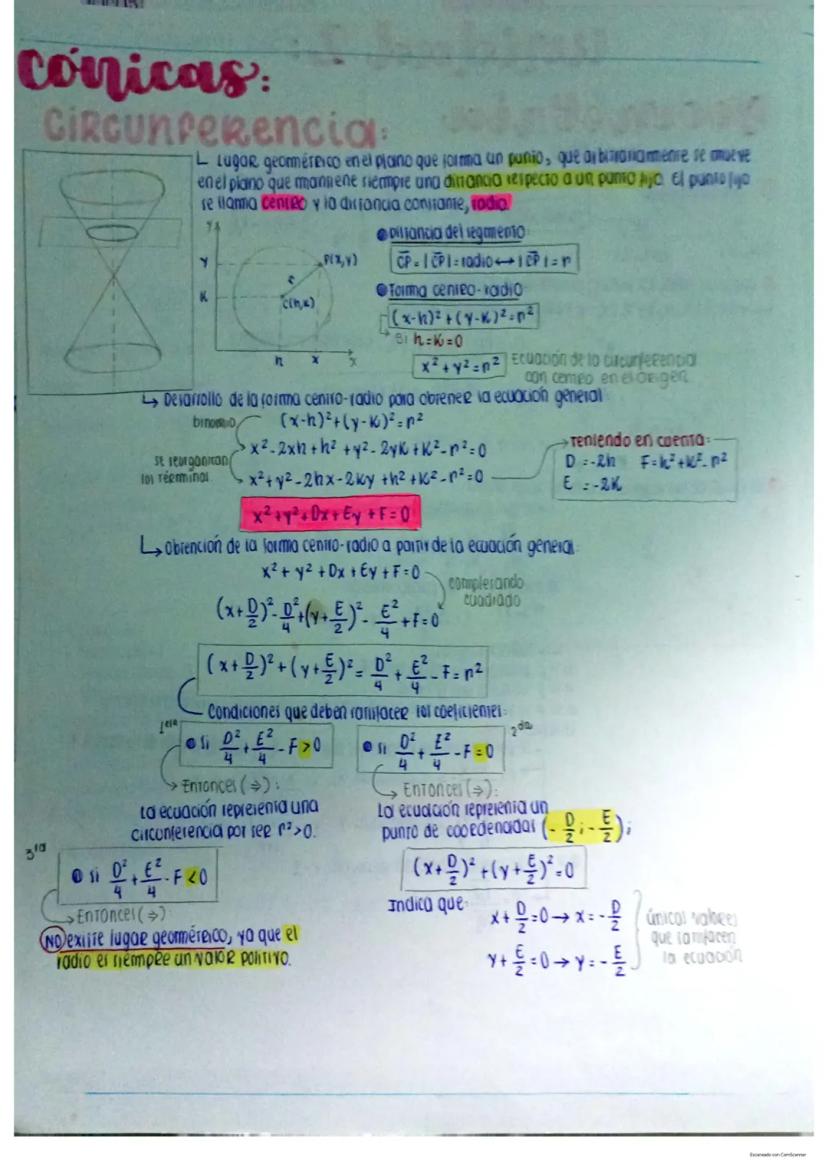
La circunferencia es el lugar geométrico de los puntos que se encuentran a una distancia constante (radio) de un punto fijo (centro). Si el centro está en $(h,k)$, su ecuación es:

$(x-h)^2 + (y-k)^2 = r^2$

Cuando el centro está en el origen, la ecuación se simplifica a:

$x^2 + y^2 = r^2$

Para obtener la ecuación general, desarrollamos la ecuación de forma centro-radio:

$x^2 + y^2 - 2hx - 2ky + h^2 + k^2 - r^2 = 0$

Que se puede escribir como:

$x^2 + y^2 + Dx + Ey + F = 0$

donde $D = -2h$, $E = -2k$ y $F = h^2 + k^2 - r^2$.

A partir de la ecuación general, podemos identificar tres casos:

1. Si $D^2 + E^2 - 4F > 0$: la ecuación representa una circunferencia
2. Si $D^2 + E^2 - 4F = 0$: la ecuación representa un punto
3. Si $D^2 + E^2 - 4F < 0$: no existe lugar geométrico (no hay puntos que satisfagan la ecuación)

🔍 Completando cuadrados en la ecuación general, podemos determinar rápidamente el centro y radio: $(x+\frac{D}{2})^2 + (y+\frac{E}{2})^2 = \frac{D^2+E^2-4F}{4}$

Elipse: Elementos y Ecuaciones

La elipse es una curva cerrada donde la suma de distancias desde cualquier punto a dos puntos fijos (focos) es constante. Su ecuación estándar centrada en el origen es:

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

Cuando el centro se desplaza a $(h,k)$, la ecuación se convierte en:

$\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1$

Elementos principales:

• Centro $(h,k)$
• Semieje mayor $a$ y semieje menor $b$
• Vértices: $V_1(h+a,k)$, $V_2(h-a,k)$, $V_3(h,k+b)$, $V_4(h,k-b)$
• Focos: $F_1(h+c,k)$, $F_2(h-c,k)$ donde $c^2 = a^2 - b^2$
• Directrices: rectas paralelas al eje menor ubicadas a distancia $\frac{a^2}{c}$ de los focos
• Longitud del lado recto: $\frac{2b^2}{a}$

La elipse presenta una importante propiedad óptica: si un rayo parte de un foco, se refleja en la curva y pasa por el otro foco. Esta propiedad se demuestra probando que los ángulos de incidencia y reflexión son iguales.

🌟 Esta propiedad óptica tiene aplicaciones prácticas en la construcción de "galerías susurrantes", donde una persona parada en un foco puede escuchar claramente a alguien que susurra desde el otro foco, incluso a gran distancia.

Propiedad Óptica de la Elipse

La fascinante propiedad óptica de la elipse establece que cualquier rayo que emerge de un foco, al reflejarse según la recta tangente, pasará por el otro foco. Esta propiedad tiene aplicaciones importantes en óptica y acústica.

Para demostrar matemáticamente esta propiedad, debemos probar que los ángulos α (incidencia) y β (reflexión) son iguales.

El proceso de demostración incluye:

1. Encontrar la ecuación de la recta tangente a la elipse en un punto $P(x_0,y_0)$ derivando implícitamente la ecuación de la elipse: $\frac{2x}{a^2} + \frac{2yy'}{b^2} = 0$

   Despejando la derivada, obtenemos la pendiente de la tangente: $m = -\frac{b^2x_0}{a^2y_0}$

2. Calcular los ángulos entre esta recta tangente y las rectas que unen el punto $P$ con los focos.

3. Aplicar la fórmula del ángulo entre dos rectas: $\tan(\alpha) = \frac{m-m_1}{1+mm_1}$

4. Tras realizar los cálculos algebraicos correspondientes, se demuestra que $\tan(\alpha) = -\frac{b^2}{cy_0}$ y $\tan(\beta) = \frac{b^2}{cy_0}$

5. Como $\tan(\alpha) = -\tan(\beta)$, se concluye que $\alpha = \beta$

Las ecuaciones paramétricas de la elipse son:

• $x = x_0 + a\cos\theta$
• $y = y_0 + b\sin\theta$

🔍 Esta demostración puede parecer compleja, pero nos revela algo hermoso: la naturaleza sigue principios matemáticos precisos. Las propiedades reflexivas de la elipse se utilizan en litotriptores (para eliminar cálculos renales) y en el diseño de algunos telescopios reflectores.

Elipse: Desarrollo de la Ecuación Canónica

La elipse se define geométricamente como el lugar geométrico de puntos cuya suma de distancias a dos puntos fijos (focos) es constante. Esta definición nos permite derivar su ecuación canónica mediante pasos algebraicos.

Partiendo de la definición $PF_1 + PF_2 = 2a$, donde $P(x,y)$ es un punto de la elipse y $F_1(-c,0)$ y $F_2(c,0)$ son los focos:

1. Expresamos las distancias usando la fórmula de distancia: $\sqrt{(x-c)^2 + y^2} + \sqrt{(x+c)^2 + y^2} = 2a$

2. Elevamos al cuadrado y realizamos manipulaciones algebraicas: $\sqrt{(x-c)^2 + y^2} = 2a - \sqrt{(x+c)^2 + y^2}$ $(x-c)^2 + y^2 = 4a^2 - 4a\sqrt{(x+c)^2 + y^2} + (x+c)^2 + y^2$

3. Simplificamos y resolvemos para obtener: $c^2x^2 + a^4 = a^2x^2 + a^2c^2 + a^2y^2$ $a^2(a^2 - c^2) = a^2y^2 + x^2(a^2 - c^2)$

4. Definimos $b^2 = a^2 - c^2$, lo que nos permite escribir: $a^2b^2 = a^2y^2 + b^2x^2$

5. Dividiendo por $a^2b^2$, obtenemos la ecuación canónica: $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

Esta ecuación nos muestra que la elipse intersecta:

• El eje x en $(\pm a, 0)$
• El eje y en $(0, \pm b)$

Además, la curva está acotada dentro del rectángulo definido por $-a \leq x \leq a$ y $-b \leq y \leq b$.

💡 La relación $b^2 = a^2 - c^2$ tiene un significado geométrico: cuanto más cerca estén los focos entre sí (menor $c$), más se acercará la elipse a una circunferencia donde $a = b$ y $c = 0$.

Elipse: Intersecciones y Acotaciones

La elipse es una curva cerrada y acotada, lo que significa que está contenida dentro de un rectángulo bien definido. Al analizar su ecuación canónica $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, podemos determinar sus límites y puntos clave.

Intersecciones con los ejes coordenados:

1. Intersección con el eje x $y = 0$:

   • $\frac{x^2}{a^2} = 1 \implies x = \pm a$
   • Puntos: $V_1(a,0)$ y $V_2(-a,0)$

2. Intersección con el eje y $x = 0$:

   • $\frac{y^2}{b^2} = 1 \implies y = \pm b$
   • Puntos: $V_3(0,b)$ y $V_4(0,-b)$

Acotaciones de la curva:

En el eje x:

• Para que $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ tenga solución real, necesitamos $\frac{x^2}{a^2} \leq 1$
• Esto implica que $-a \leq x \leq a$

En el eje y:

• De manera similar, $\frac{y^2}{b^2} \leq 1$
• Por lo tanto, $-b \leq y \leq b$

Cuando la elipse tiene su centro desplazado a un punto $(h,k)$, su ecuación se convierte en: $\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1$

Para trabajar con esta ecuación, podemos establecer un nuevo sistema de coordenadas con origen en $(h,k)$ y ejes paralelos a los originales.

🔍 La elipse representa la trayectoria de muchos cuerpos en el universo, como los planetas alrededor del sol. Kepler descubrió que estas órbitas son elípticas, con el sol ubicado en uno de los focos, no en el centro. ¡Un ejemplo perfecto de cómo la geometría describe el mundo real!

Parábola: Definición y Ecuaciones Básicas

La parábola es el conjunto de puntos del plano que equidistan de un punto fijo (foco) y una recta fija (directriz). Esta definición geométrica es la base para todas sus propiedades y aplicaciones.

Elementos principales:

• Vértice $(h,k)$: punto donde la parábola cambia de dirección
• Foco: punto que se encuentra en el eje de simetría a una distancia $p$ del vértice
• Directriz: línea perpendicular al eje de simetría, situada a una distancia $p$ del vértice
• Lado recto: cuerda perpendicular al eje de simetría que pasa por el foco, con longitud $|4p|$

Cuando el vértice coincide con el origen, podemos tener dos casos:

1. Parábola vertical con foco en $(0,p)$:

   • Ecuación: $x^2 = 4py$
   • Si $p > 0$, la parábola abre hacia arriba
   • Si $p < 0$, la parábola abre hacia abajo

2. Parábola horizontal con foco en $(p,0)$:

   • Ecuación: $y^2 = 4px$
   • Si $p > 0$, la parábola abre hacia la derecha
   • Si $p < 0$, la parábola abre hacia la izquierda

Para derivar estas ecuaciones, partimos de la definición de equidistancia:

• Para un punto $P(x,y)$ en la parábola
• La distancia $PF$ al foco es $\sqrt{x^2+(y-p)^2}$
• La distancia $PQ$ a la directriz es $(y+p)$
• Igualando ambas y resolviendo, obtenemos $x^2 = 4py$

💡 El parámetro $p$ no solo determina la posición del foco y la directriz, sino también qué tan "abierta" es la parábola. Un valor pequeño de $|p|$ produce una parábola cerrada, mientras que un valor grande produce una parábola más abierta.