Introducción a Cálculo I

Este material ha sido desarrollado por los docentes de la Universidad Nacional de Río Cuarto para las carreras de Ingeniería en Telecomunicaciones, Química, Mecánica, Energía Eléctrica y Energías Renovables.

El tomo teórico-práctico que estás por explorar fue inicialmente recopilado por el Prof. Hugo Omar Pajello, con colaboraciones de numerosos profesores del departamento, y sigue siendo actualizado constantemente por el equipo docente actual.

¡Dato clave! Este material no solo te servirá para aprobar la asignatura, sino que construirá las bases matemáticas fundamentales que necesitarás en toda tu carrera de ingeniería.

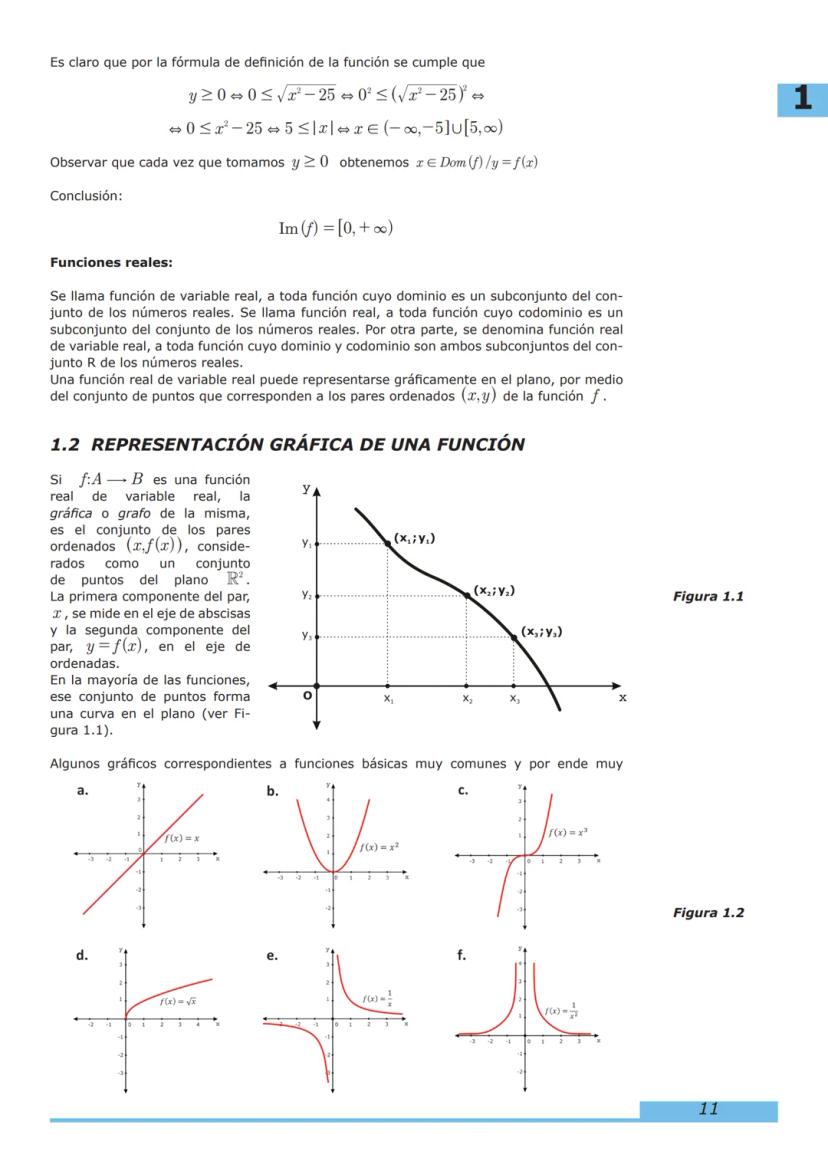
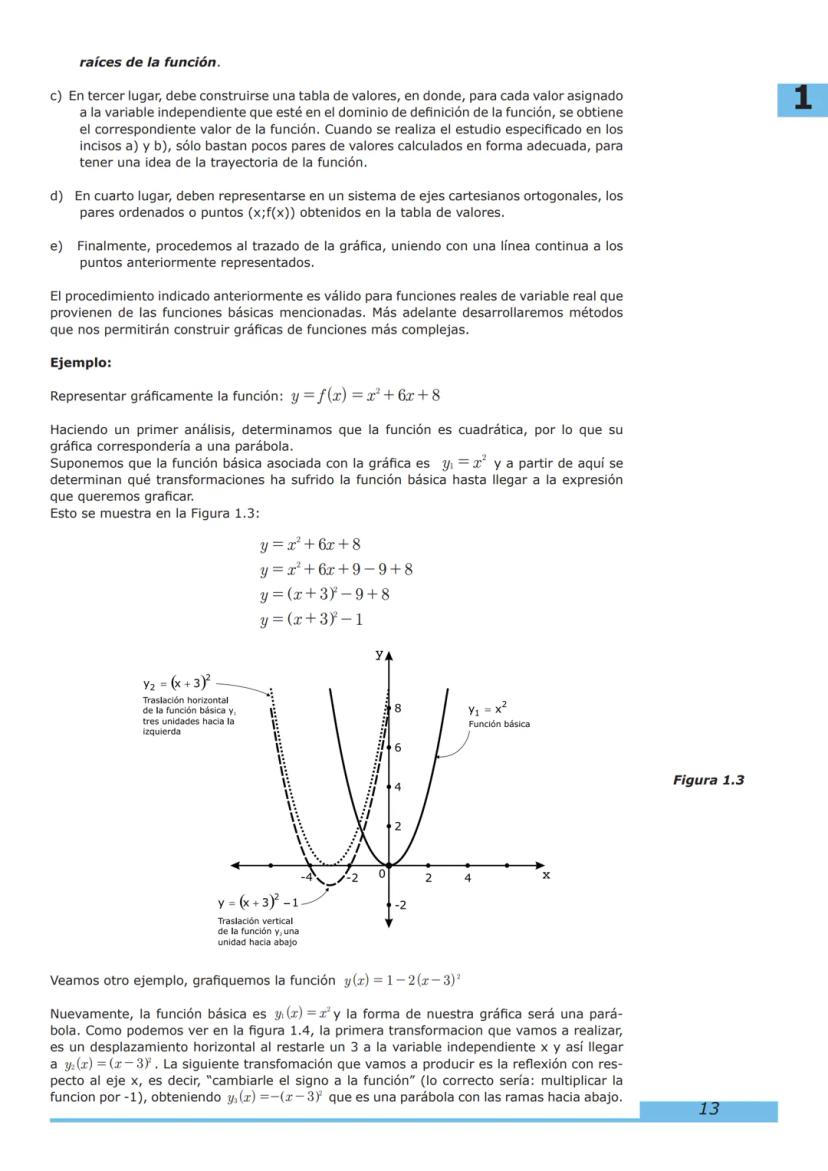
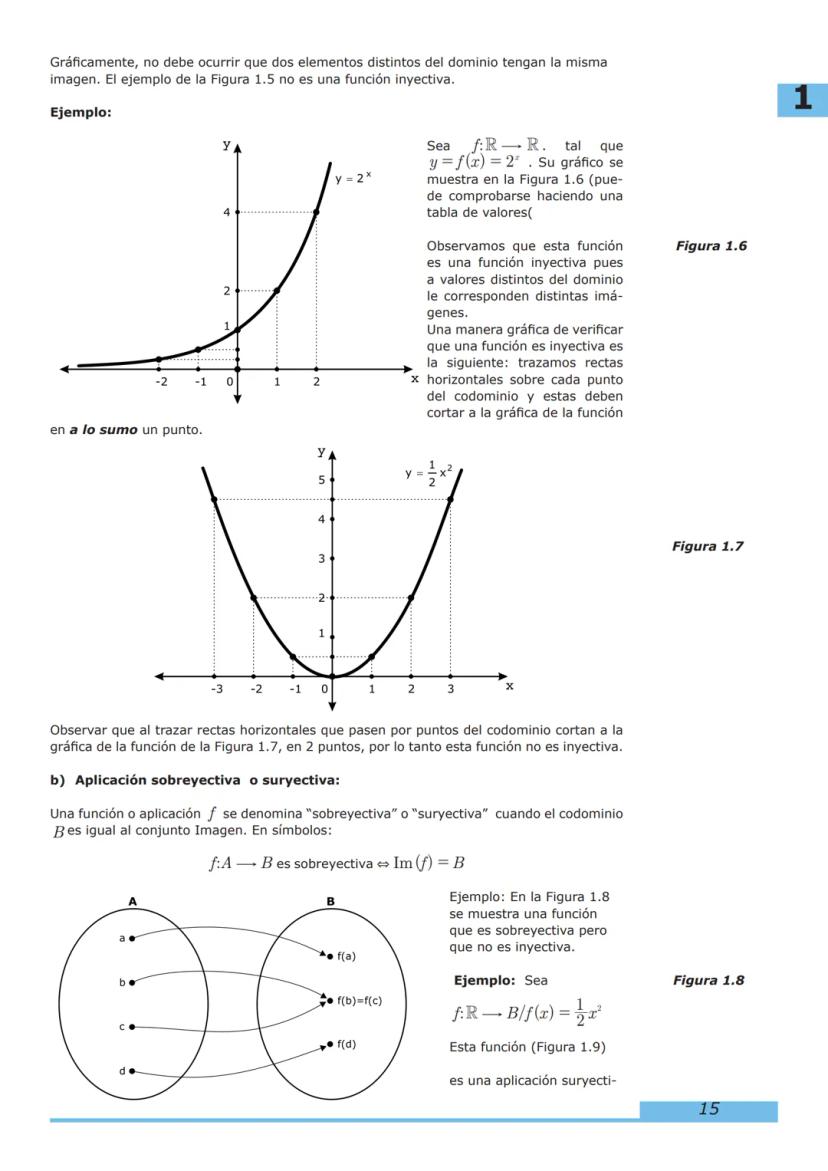
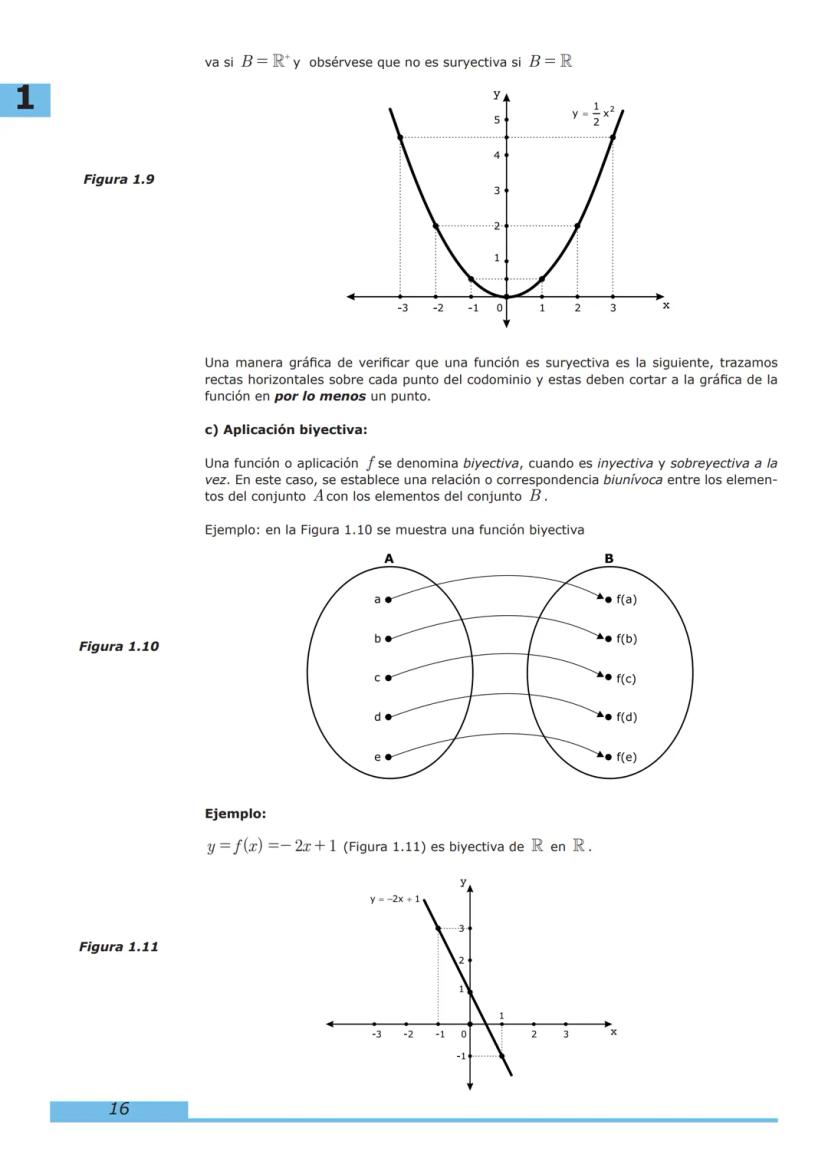
Contenido del Curso

Este curso de Cálculo I está estructurado en tres grandes bloques temáticos:

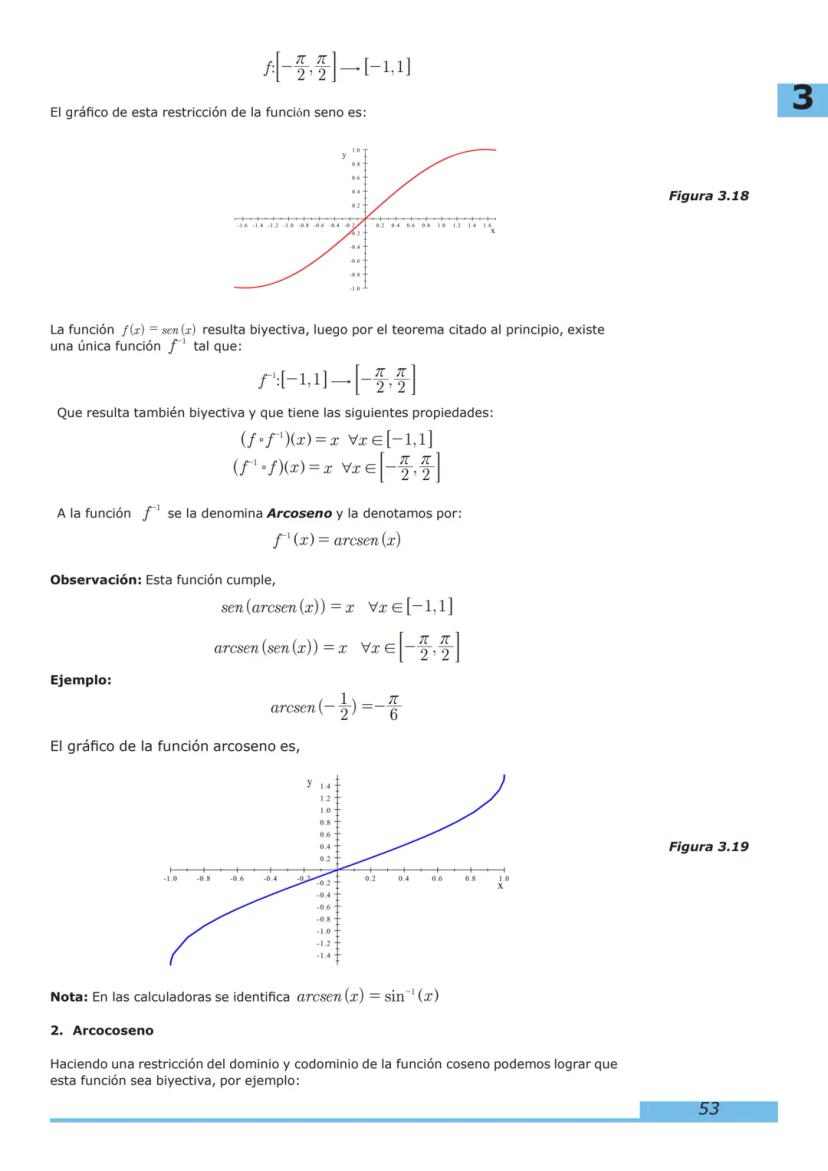
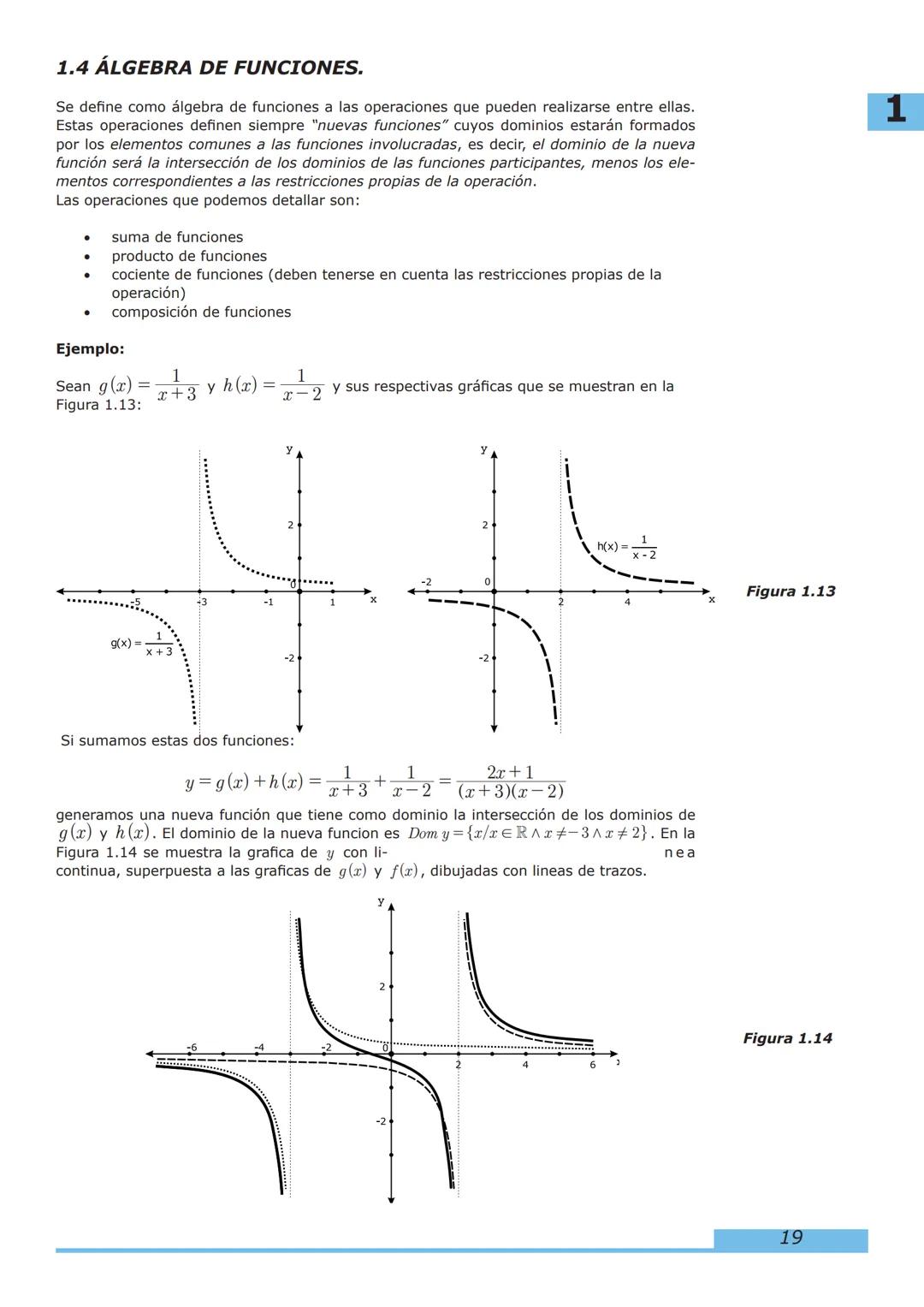
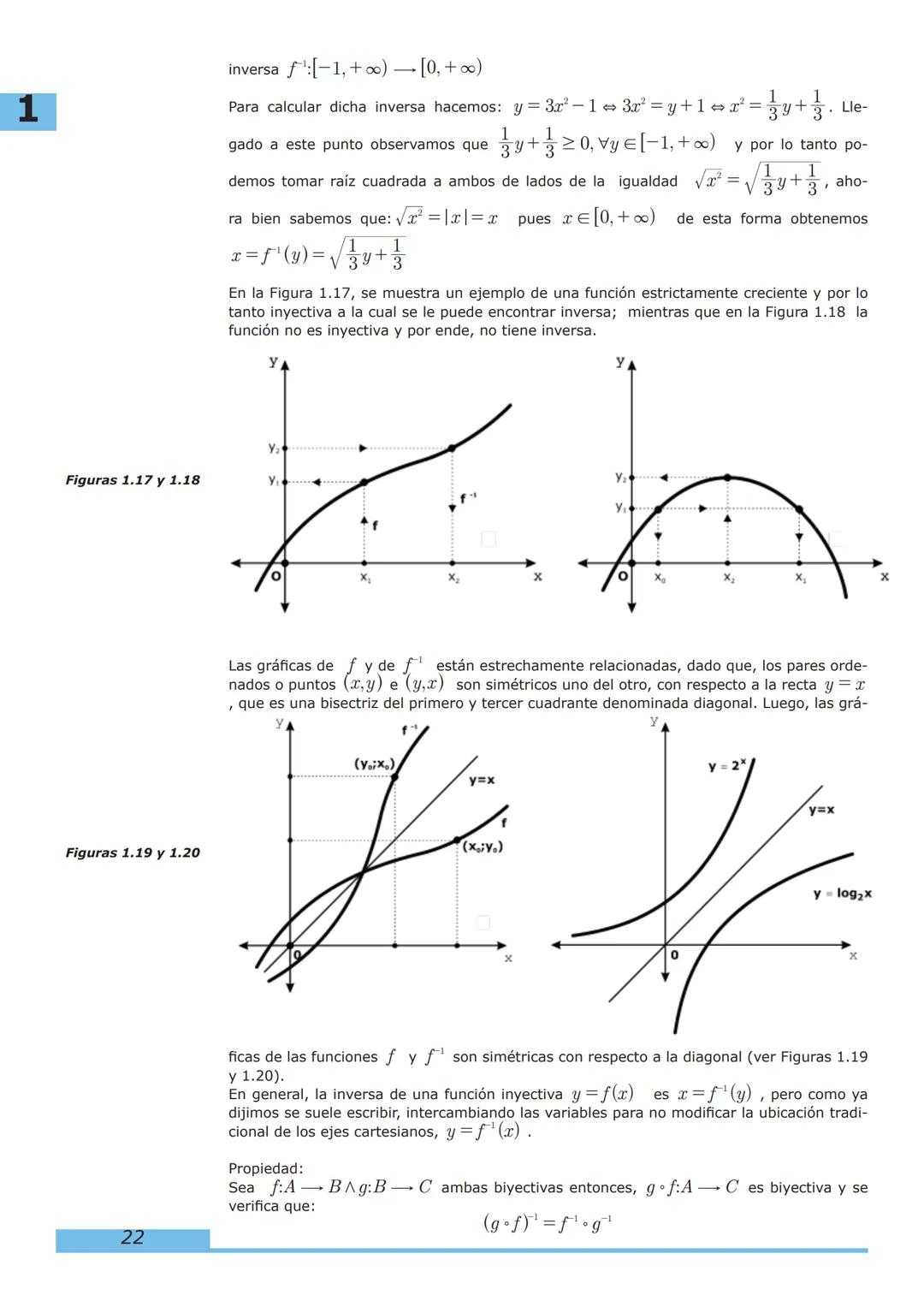
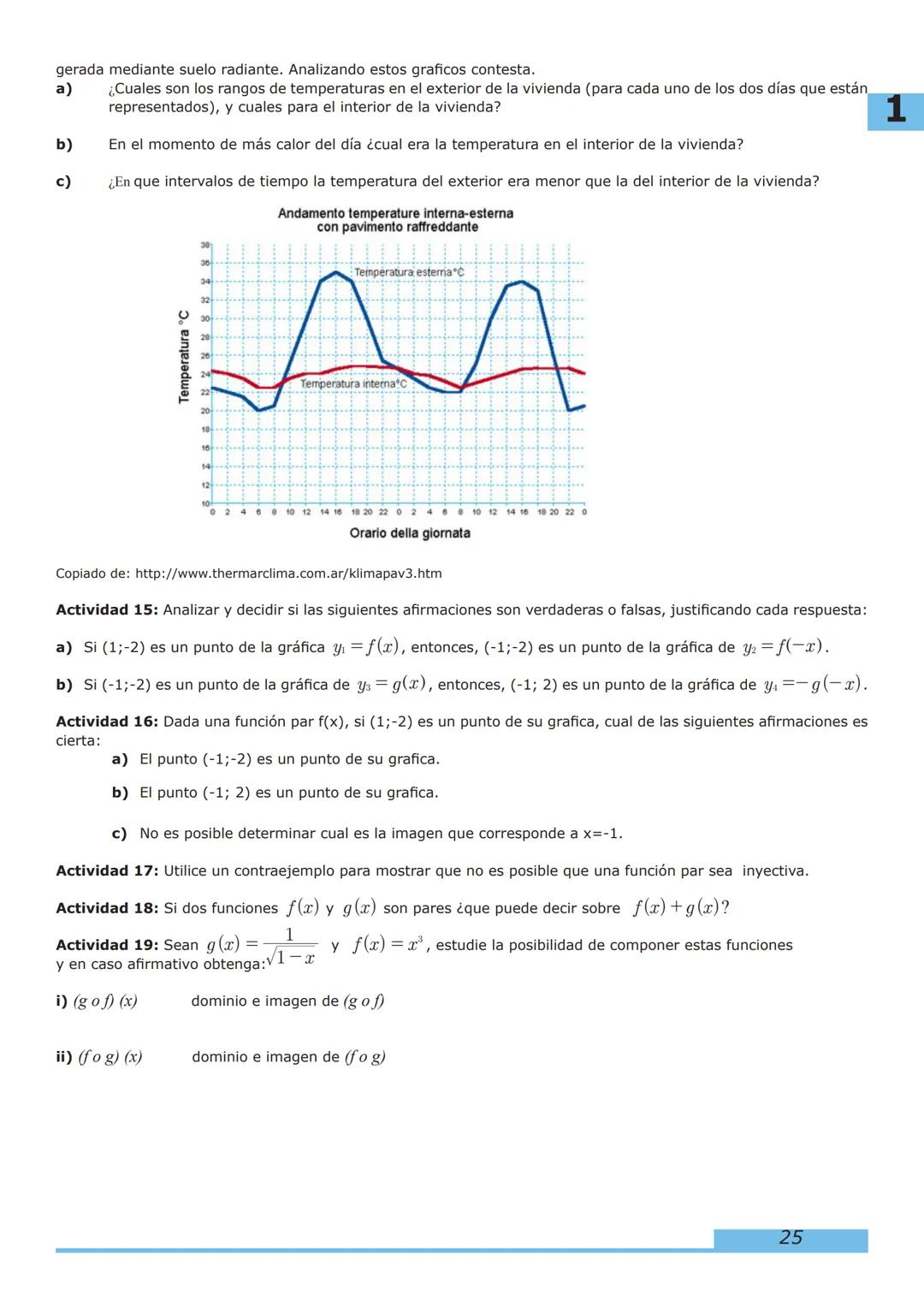
1. Funciones: Comenzaremos con las generalidades, representación gráfica, clasificación, álgebra de funciones y funciones inversas. Estos conceptos son la base de todo lo que aprenderás después.

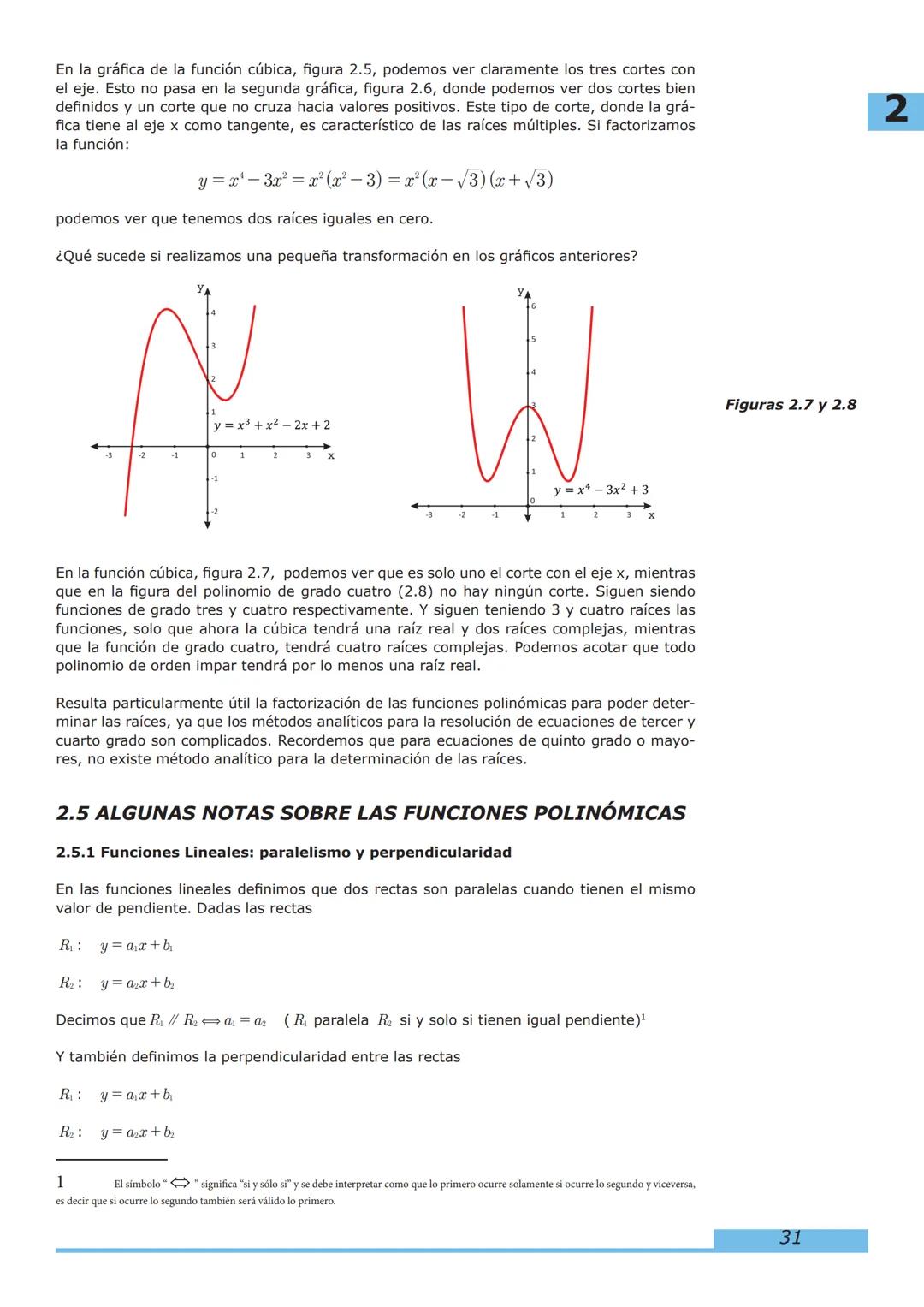
2. Funciones Algebraicas: Exploraremos funciones polinómicas, homográficas e irracionales, analizando sus características y comportamientos.

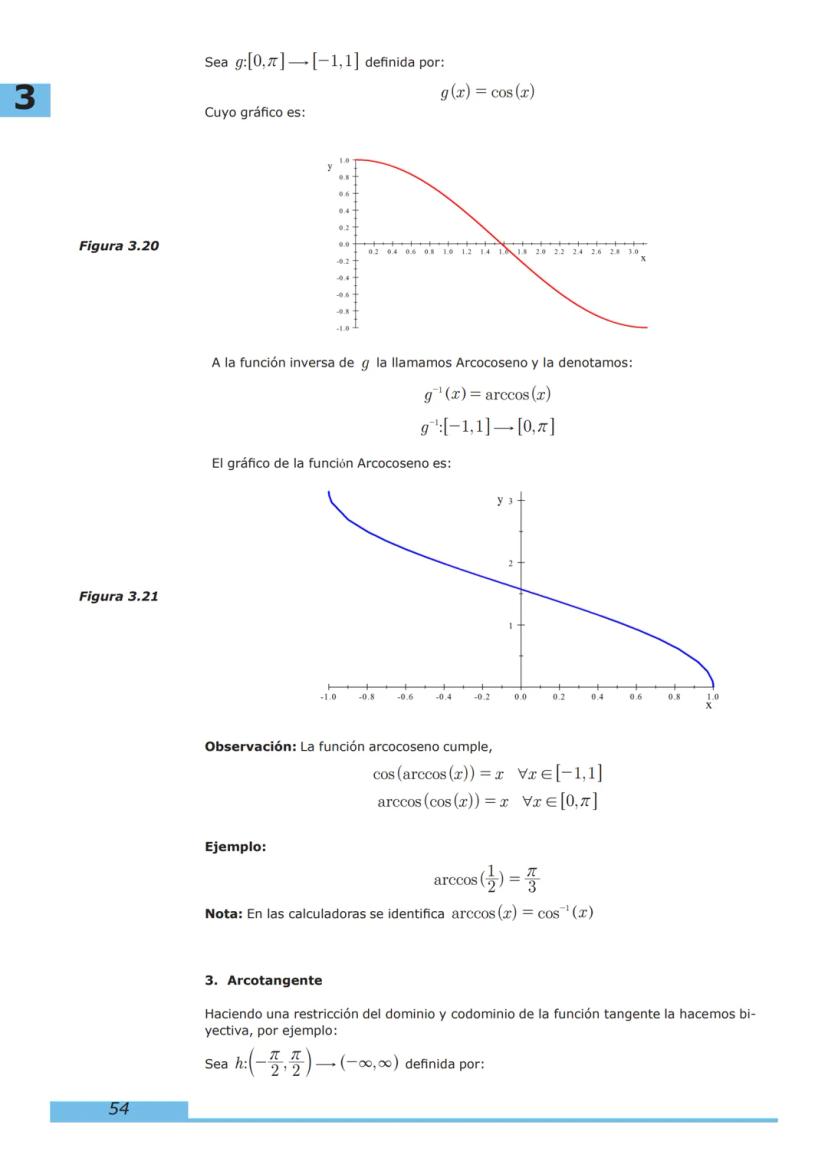
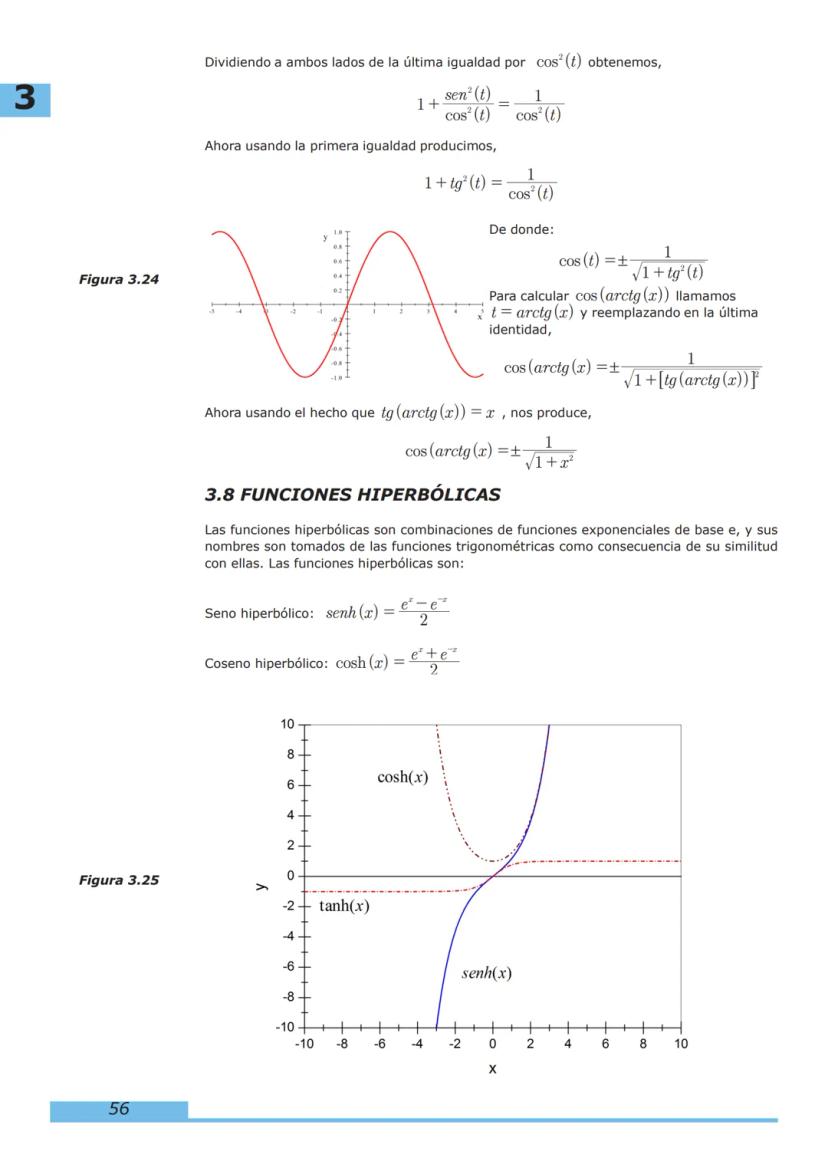
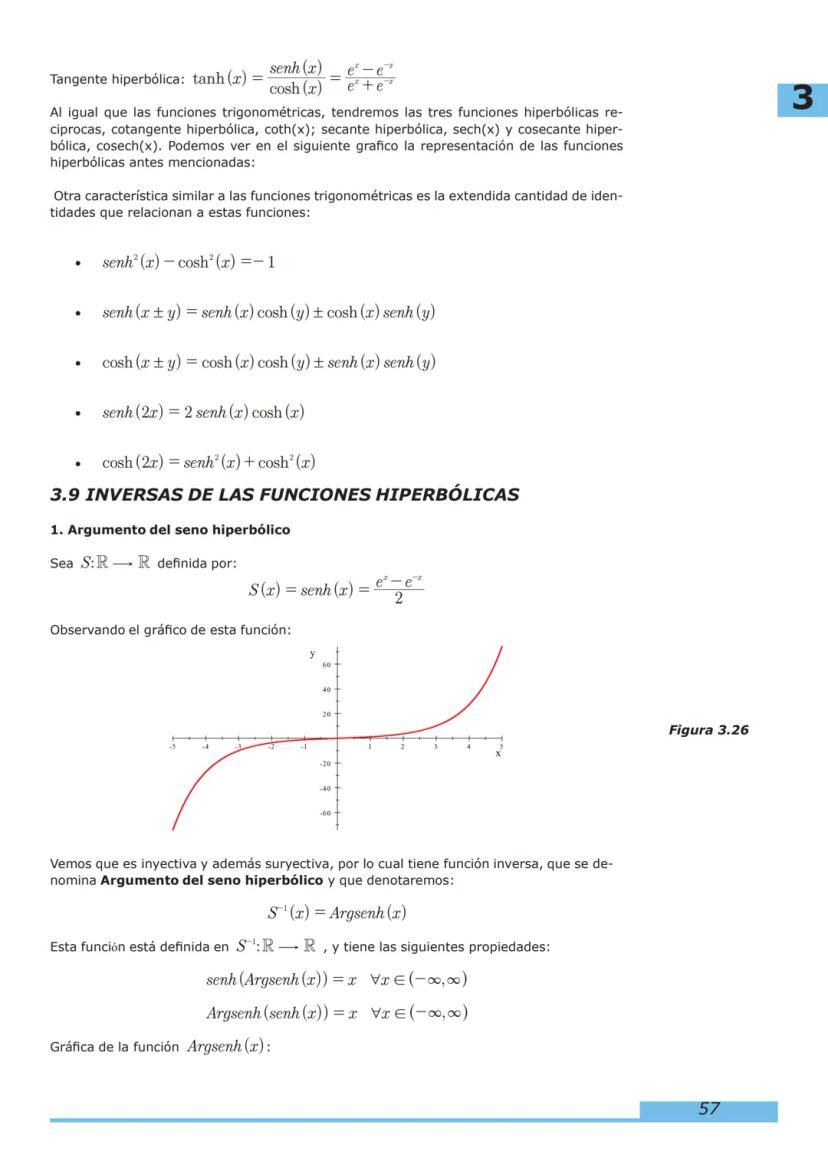
3. Funciones Trascendentes: Estudiaremos funciones exponenciales, logarítmicas, trigonométricas e hiperbólicas que tienen aplicaciones fundamentales en la ingeniería.

Cada sección incluye tanto contenido teórico como trabajos prácticos para reforzar tu aprendizaje. El material está diseñado para que puedas progresar desde conceptos básicos hasta aplicaciones más complejas.

Consejo importante: Dedica tiempo a los trabajos prácticos - la única forma de dominar el cálculo es resolviendo problemas.

Funciones: Generalidades

Una función es una relación que a cada elemento x de un conjunto A le hace corresponder un único elemento y en un conjunto B. Matemáticamente lo expresamos como:

f: A → B x → y = f(x)

Los elementos x ∈ A son los valores del argumento o variable independiente, mientras que los y ∈ B son los valores de la función o variable dependiente.

Por ejemplo, si definimos f: ℤ → ℝ como f(x) = 3x + 2, entonces:

• Para x = 1: f(1) = 3·1 + 2 = 5
• Para x = -2: f(-2) = 3(-2) + 2 = -4

Otro ejemplo sería g: ℝ → ℝ definida como g(x) = cos(x), donde:

• Para x = π/2: g(π/2) = cos(π/2) = 0
• Para x = π: g(π) = cos(π) = -1

Recordá que: Una función asocia cada elemento del dominio con exactamente un elemento del codominio, nunca con más de uno. ¡Esta es la clave para identificar correctamente una función!

Representación Gráfica de Funciones

La gráfica o grafo de una función real f: A → B es el conjunto de pares ordenados (x, f(x)) representados como puntos en el plano ℝ². El eje horizontal (abscisas) muestra los valores de x, mientras que el vertical (ordenadas) representa los valores de f(x).

Las transformaciones básicas nos permiten modificar la gráfica de una función:

• Traslación horizontal: f$x-h$ desplaza la gráfica h unidades a la derecha
• Traslación vertical: f(x)+k desplaza la gráfica k unidades hacia arriba
• Reflexión respecto al eje x: -f(x) invierte la gráfica verticalmente
• Reflexión respecto al eje y: f$-x$ invierte la gráfica horizontalmente
• Estiramiento vertical: a·f(x) (con a > 1) estira la gráfica verticalmente
• Compresión vertical: a·f(x) (con 0 < a < 1) comprime la gráfica verticalmente

Para realizar transformaciones múltiples, es importante seguir un orden correcto para obtener el resultado deseado. Generalmente, primero se aplican las transformaciones que afectan el argumento (como reflexiones horizontales) y luego las que afectan a la función completa.

Atención: Al aplicar varias transformaciones, el orden importa. Por ejemplo, sumar y luego multiplicar no da el mismo resultado que multiplicar y luego sumar.

Clasificación de Funciones

Las funciones pueden clasificarse según varios criterios:

1. Según el comportamiento de la imagen:

• Función inyectiva: Cuando a valores distintos del dominio corresponden valores distintos de la función. Gráficamente, toda recta horizontal corta a la gráfica en a lo sumo un punto.
• Función sobreyectiva: Cuando el conjunto imagen coincide con el codominio.
• Función biyectiva: Cuando es simultáneamente inyectiva y sobreyectiva.

2. Según su expresión analítica:

• Funciones algebraicas: Contienen operaciones fundamentales, potenciación y radicación (polinomios, radicales, racionales). Ejemplos: f(x) = x³ + 3x², g(x) = √$x² - 2x$
• Funciones trascendentes: No son algebraicas, como las trigonométricas, exponenciales y logarítmicas. Ejemplos: f(x) = tg(x), g(x) = e^$3x+1$

3. Según la simetría:

• Función par: Cumple f$-x$ = f(x). Su gráfica es simétrica respecto al eje y.
• Función impar: Cumple f$-x$ = -f(x). Su gráfica es simétrica respecto al origen.

Truco para recordar: Para verificar rápidamente la inyectividad de una función, dibujá su gráfica y pasá rectas horizontales. Si alguna recta corta la gráfica en más de un punto, la función no es inyectiva.

Álgebra de Funciones y Composición

El álgebra de funciones nos permite crear nuevas funciones a partir de otras mediante operaciones básicas:

• Suma: $f + g$(x) = f(x) + g(x)
• Resta: $f - g$(x) = f(x) - g(x)
• Producto: (f · g)(x) = f(x) · g(x)
• Cociente: $f/g$(x) = f(x)/g(x), donde g(x) ≠ 0

La composición de funciones es otra operación fundamental:

Dadas las funciones f: X → U y g: U → Y, donde Im(f) ⊆ Dom(g), se define la función compuesta g∘f: X → Y como:

(g∘f)(x) = g(f(x))

Esta operación no es conmutativa (generalmente g∘f ≠ f∘g) pero sí es asociativa: h∘(g∘f) = (h∘g)∘f.

Para que exista la composición, la imagen de f y el dominio de g deben tener elementos en común. Si Im(f) ∩ Dom(g) = ∅, entonces g∘f no existe.

Importante: La composición de funciones aparece constantemente en cálculo avanzado. Cuando veas expresiones como f(g(x)), estás ante una composición. ¡Dominar este concepto te dará ventaja en muchos problemas!

Funciones Inversas

Una función f: A → B tiene función inversa si y solo si es biyectiva (inyectiva y sobreyectiva).

La función inversa de f, denotada como f^(-1): B → A, cumple que:

• f^(-1)(f(x)) = x para todo x ∈ A
• f$f^(-1)(y)$ = y para todo y ∈ B

Gráficamente, la función inversa se obtiene reflejando la gráfica de f respecto a la recta y = x.

Si f no es biyectiva en todo su dominio, podemos restringir su dominio para hacerla biyectiva y así obtener una función inversa en ese dominio restringido.

Propiedades importantes:

1. $f^(-1)$^(-1) = f
2. Si f y g son biyectivas, entonces (g∘f)^(-1) = f^(-1)∘g^(-1)
3. Si f es estrictamente creciente o decreciente, entonces f es inyectiva

Para encontrar algebraicamente f^(-1), se despeja x en términos de y en la ecuación y = f(x), y luego se intercambian las variables.

Dato útil: Cuando trabajamos con funciones inversas, los dominios y las imágenes se intercambian. El dominio de f^(-1) es la imagen de f, y la imagen de f^(-1) es el dominio de f.

Funciones Polinómicas

Las funciones polinómicas tienen la forma: P(x) = a₀ + a₁x + a₂x² + ... + aₙxⁿ

donde n es un entero no negativo y aₙ ≠ 0. El coeficiente aₙ se llama coeficiente principal y n es el grado del polinomio.

Tipos especiales de polinomios:

• Función constante (grado 0): P(x) = a₀
• Función lineal (grado 1): P(x) = a₁x + a₀
• Función cuadrática (grado 2): P(x) = a₂x² + a₁x + a₀
• Función cúbica (grado 3): P(x) = a₃x³ + a₂x² + a₁x + a₀

Las gráficas de las funciones polinómicas tienen características según su grado:

• Los polinomios de grado par tienen gráficas que tienden a +∞ o -∞ en ambos extremos
• Los polinomios de grado impar tienen gráficas que tienden a +∞ en un extremo y -∞ en el otro

Las raíces de un polinomio son los valores de x para los que P(x) = 0. Según el teorema fundamental del álgebra, un polinomio de grado n tiene exactamente n raíces (contando multiplicidades), reales o complejas.

Consejo práctico: Para analizar el comportamiento de una función polinómica, identificá primero su grado y el signo del coeficiente principal. Esto te dará una idea general de cómo se comporta la función para valores muy grandes (positivos o negativos) de x.

Funciones Homográficas e Irracionales

Funciones homográficas: Son funciones de la forma: f(x) = $ax + b$/$cx + d$

donde a, b, c, d son constantes y $ad - bc$ ≠ 0 y cx + d ≠ 0.

Características importantes:

• Tienen asíntotas verticales en x = -d/c (donde el denominador se anula)
• Presentan asíntotas horizontales en y = a/c cuando |x| → ∞
• El caso más simple es f(x) = 1/x, con asíntotas en los ejes cartesianos

Funciones irracionales: Son aquellas que contienen raíces en su expresión analítica, como: f(x) = √$x - 1$ o g(x) = ∛$x + 1$

Para funciones con raíces de índice par:

• El dominio está restringido a valores donde el radicando es no negativo
• Por ejemplo, para f(x) = √$x - 1$, el dominio es x ≥ 1

Para funciones con raíces de índice impar:

• El dominio generalmente es ℝ, pues pueden tomar argumentos positivos y negativos
• Por ejemplo, para g(x) = ∛$x + 1$, el dominio es todos los números reales

Dato importante: Al trabajar con funciones homográficas, siempre identifica primero las asíntotas. Estas te darán una "estructura" sobre la cual construir la gráfica completa.

Funciones Exponenciales

La función exponencial se define como: f(x) = aˣ con a > 0 y a ≠ 1

Características de la función exponencial:

• Su dominio es ℝ y su imagen es (0, +∞)
• Es siempre positiva: f(x) > 0 para todo x
• Para a > 1:
  • Es estrictamente creciente
  • f(0) = 1
  • Para x < 0: 0 < f(x) < 1
  • Para x > 0: f(x) > 1
  • Cuando x → -∞, f(x) → 0
  • Cuando x → +∞, f(x) → +∞
• Para 0 < a < 1:
  • Es estrictamente decreciente
  • f(0) = 1
  • Para x < 0: f(x) > 1
  • Para x > 0: 0 < f(x) < 1
  • Cuando x → -∞, f(x) → +∞
  • Cuando x → +∞, f(x) → 0

La función exponencial más importante es f(x) = eˣ, donde e ≈ 2.718281... (número de Euler).

Las funciones exponenciales tienen amplias aplicaciones en:

• Crecimiento poblacional
• Interés compuesto
• Decaimiento radioactivo
• Propagación de enfermedades

Aplicación práctica: Si estás estudiando el crecimiento bacteriano, la función exponencial es tu mejor amiga. Una población que se duplica cada hora puede modelarse con f(t) = N₀·2^t, donde N₀ es la población inicial.