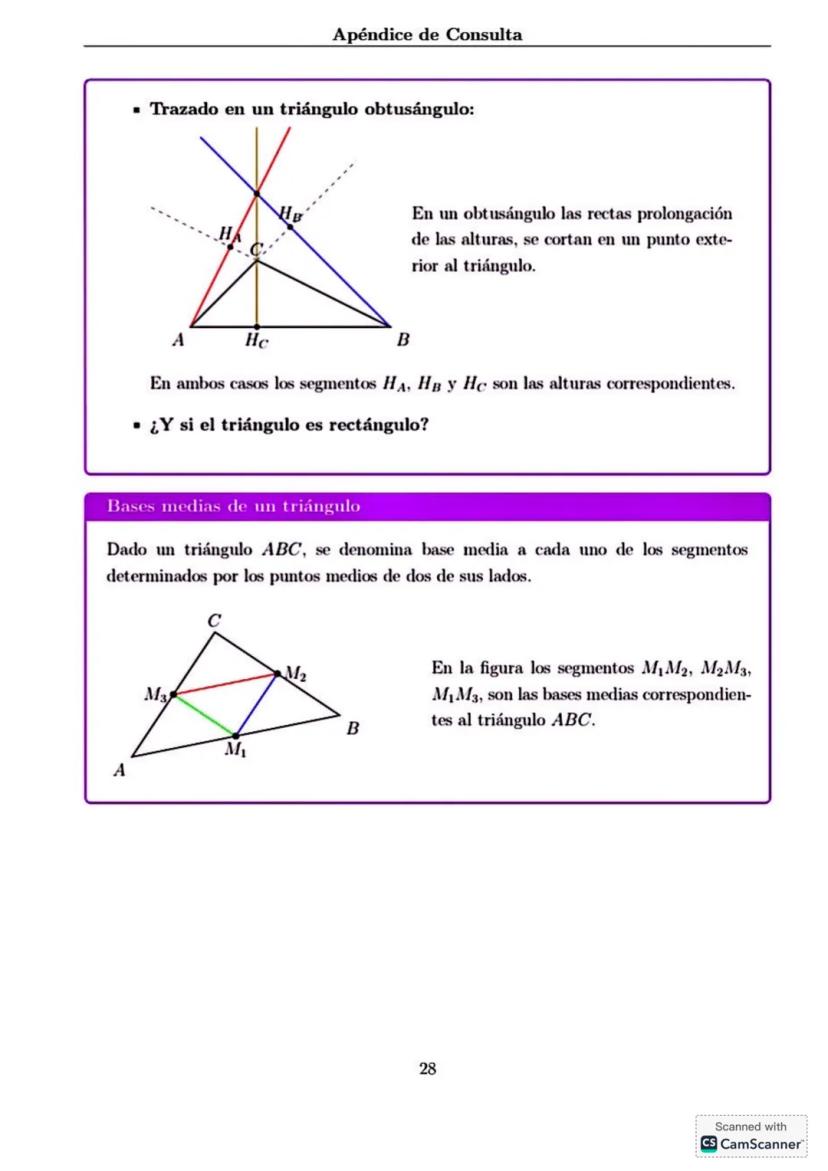
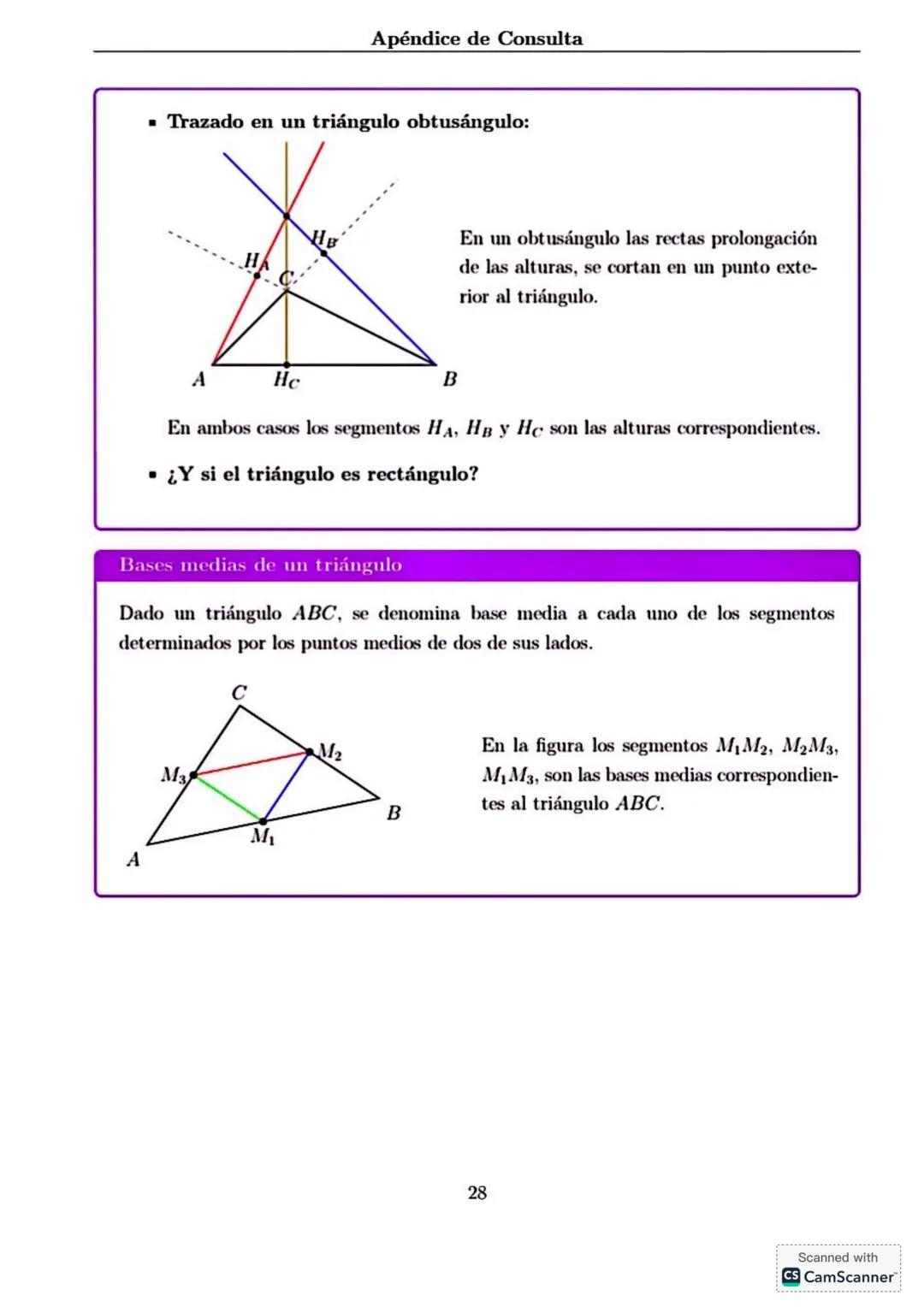
Trabajando con Valor Absoluto
El valor absoluto es súper útil para resolver problemas de distancia. Si querés todos los enteros cuyo valor absoluto es 7, la respuesta es 7 y -7 (ambos están a distancia 7 del cero).
Para números cuya distancia al origen es menor que 7, tenés: -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6. Son todos los que están "entre" -7 y 7.
Para distancia mayor o igual que 7, tenés todos los números desde -7 hacia la izquierda (..., -9, -8, -7) y desde 7 hacia la derecha (7, 8, 9, ...).
Visualízalo: Dibujá siempre una recta numérica cuando trabajés con valor absoluto. Te va a facilitar mucho la comprensión.