Funciones Especiales: Inyectivas y Monótonas
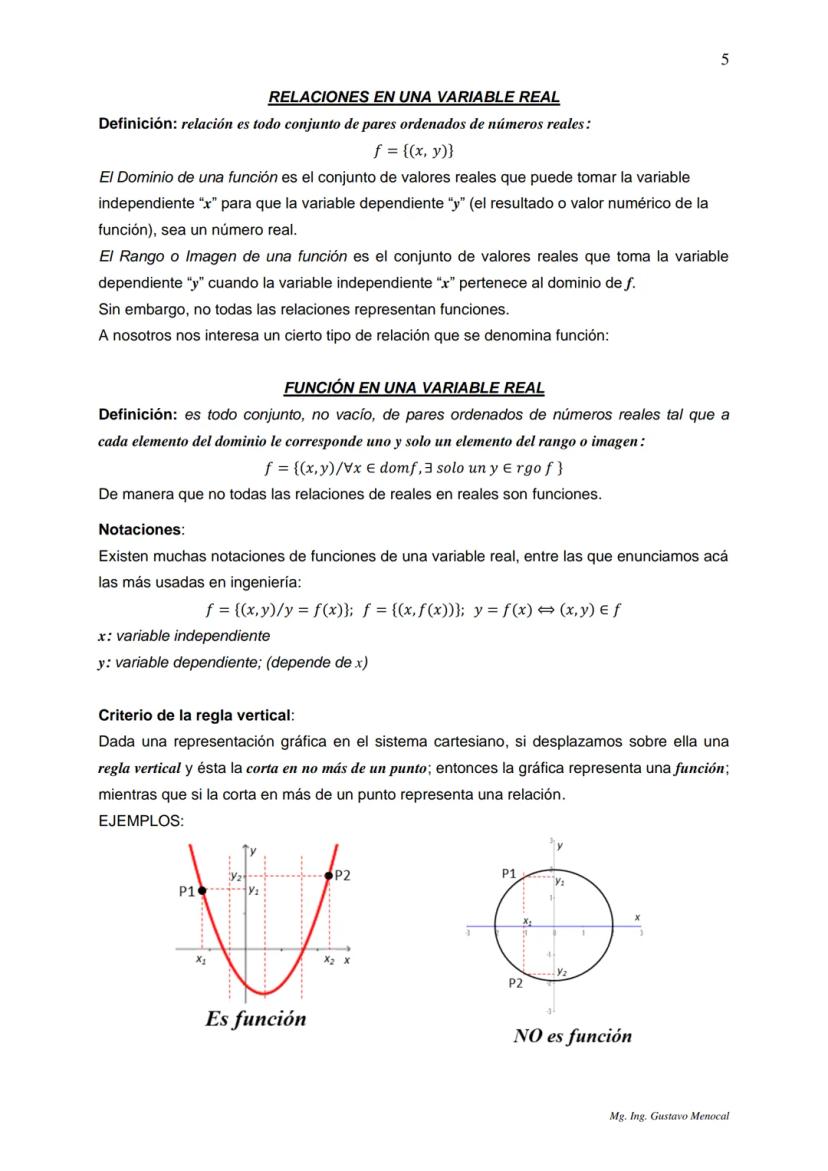
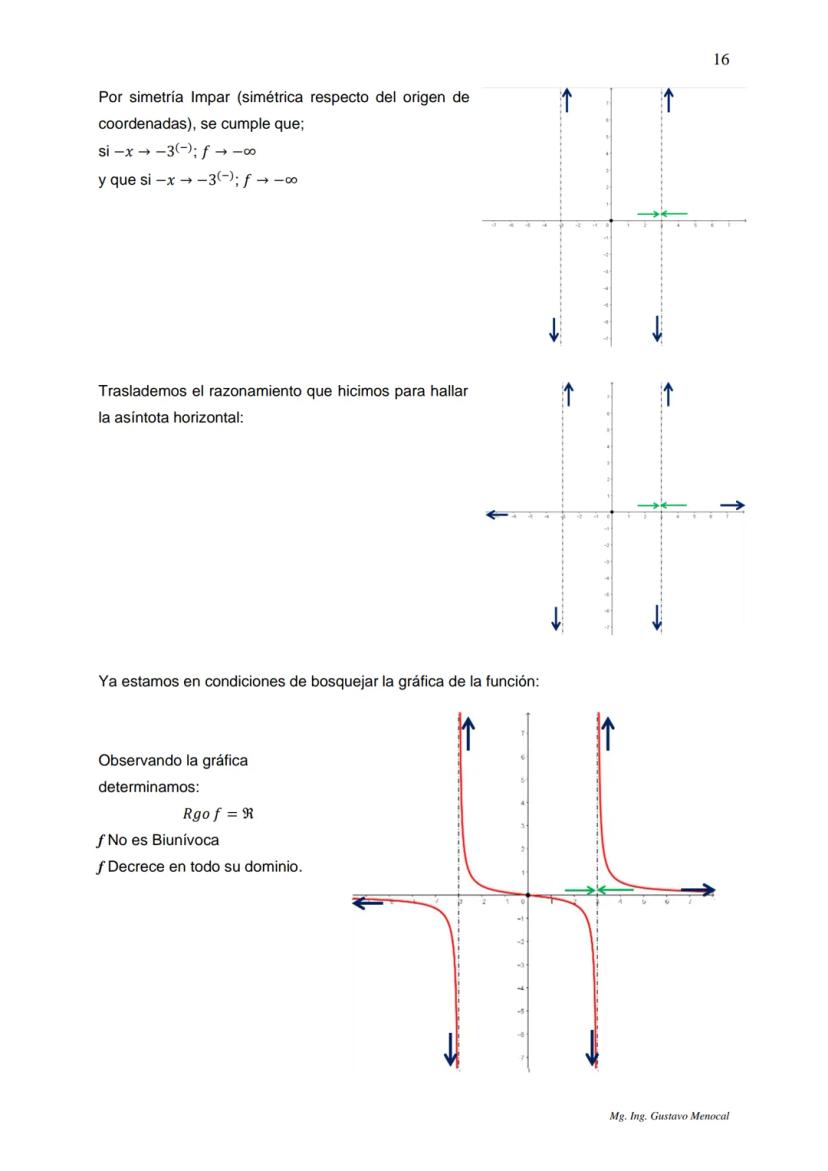
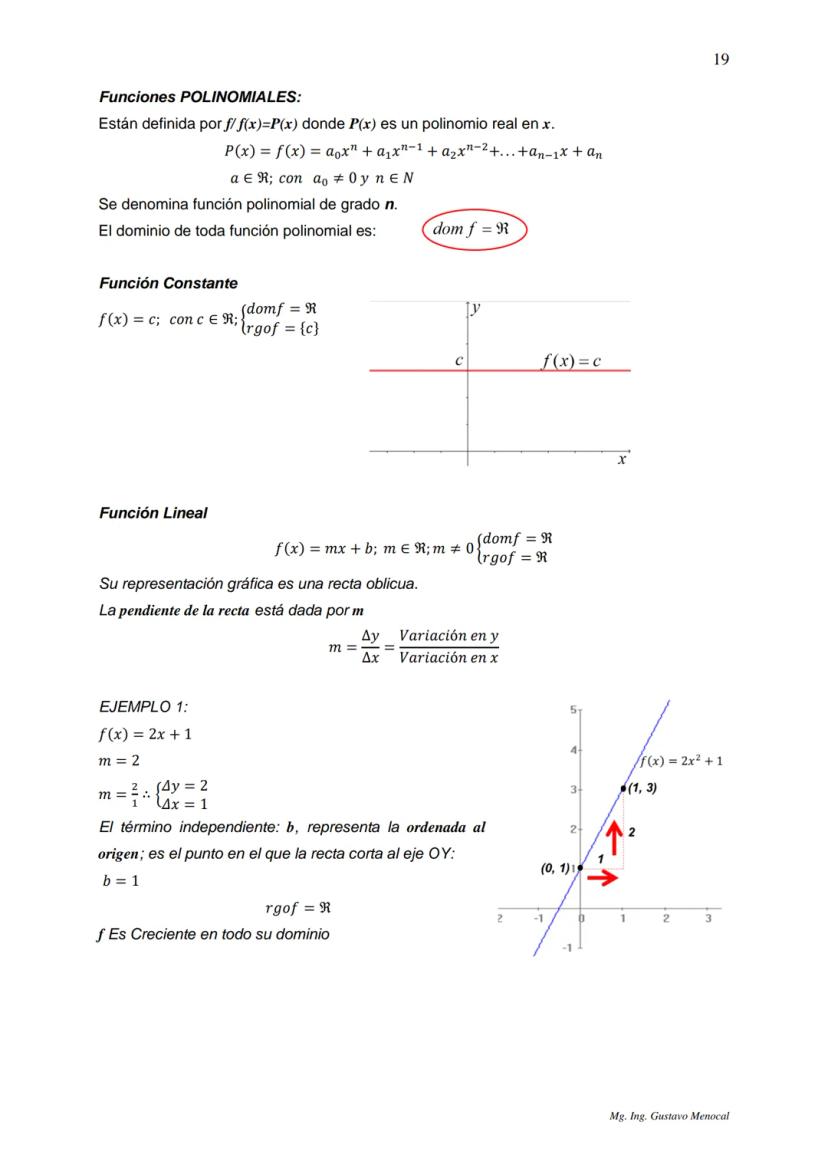
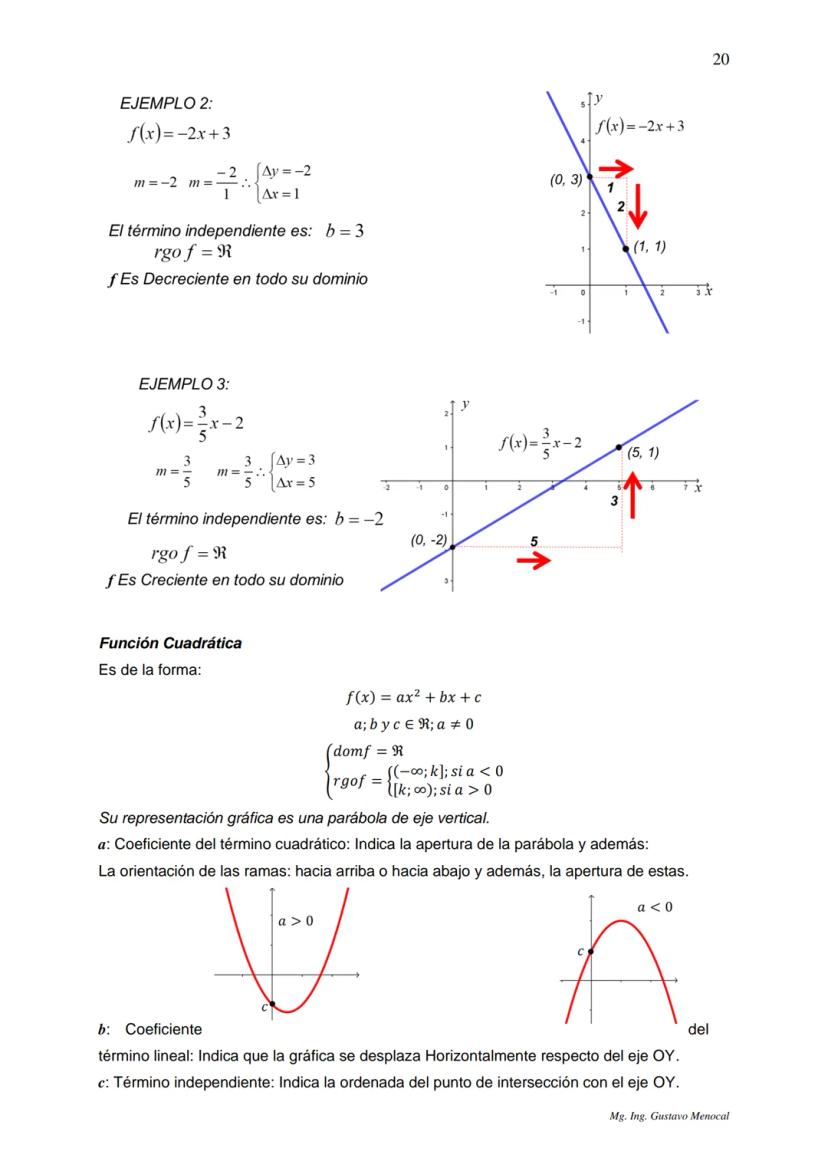
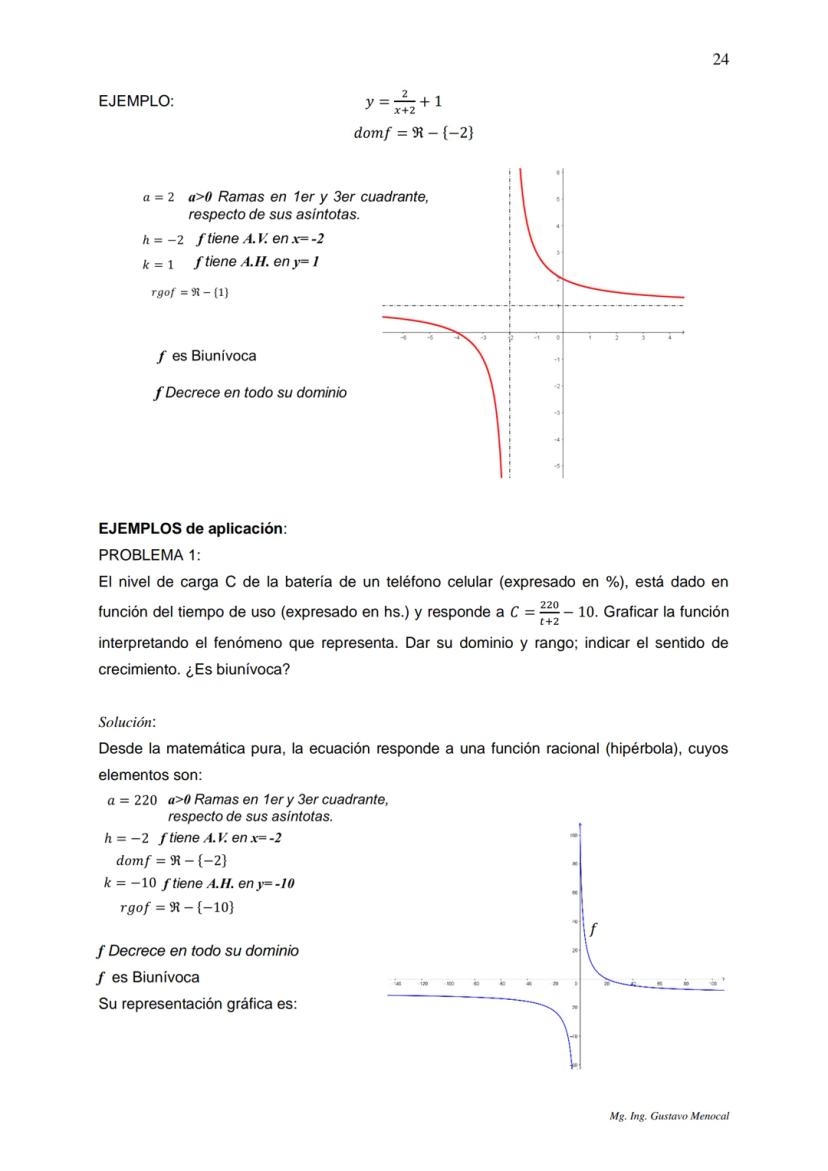
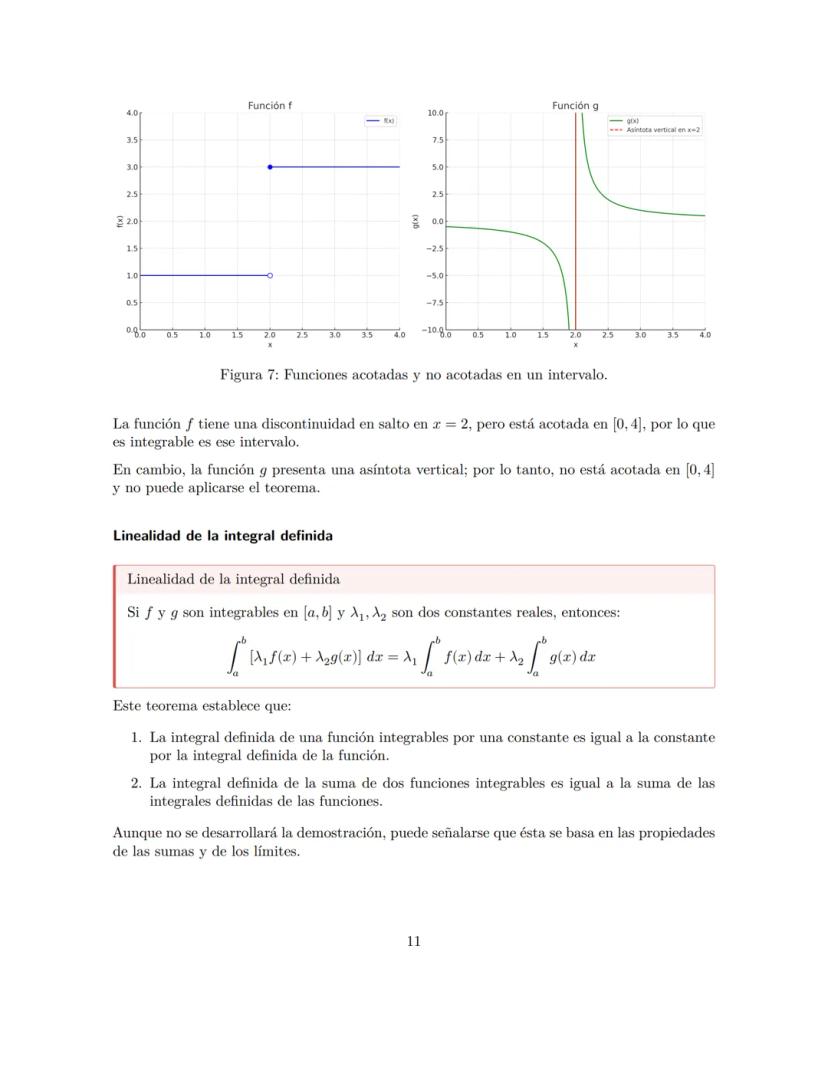
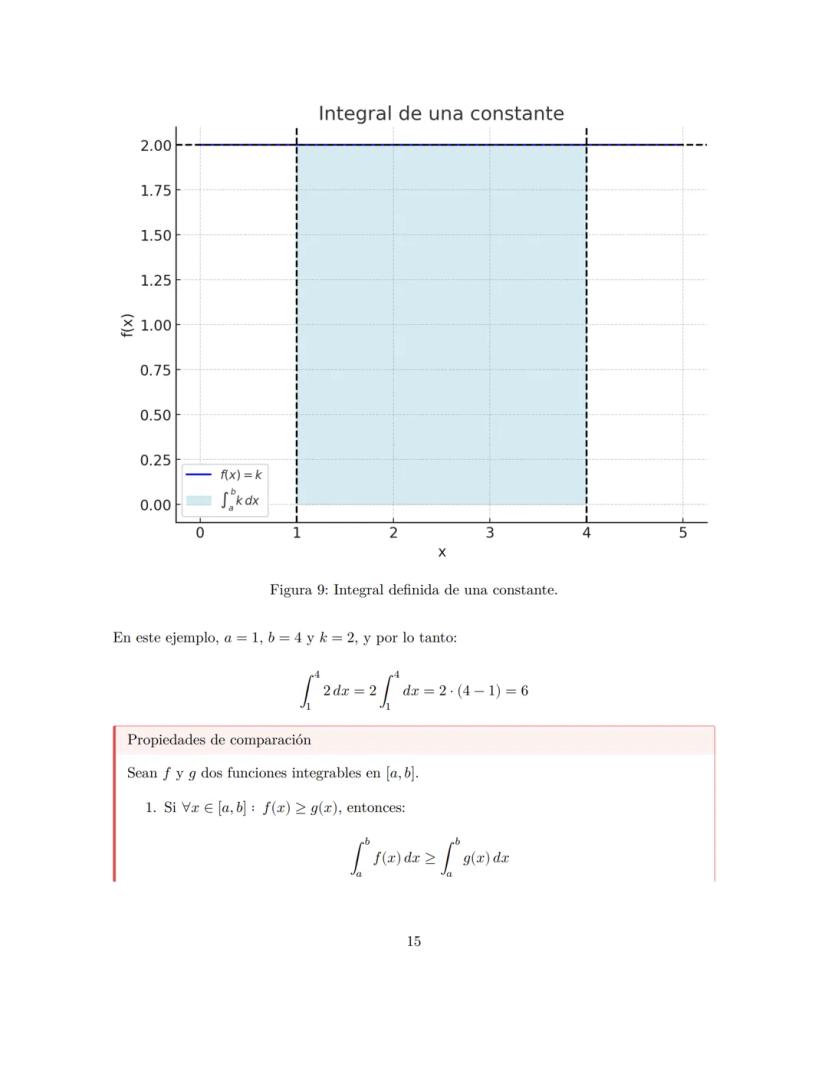
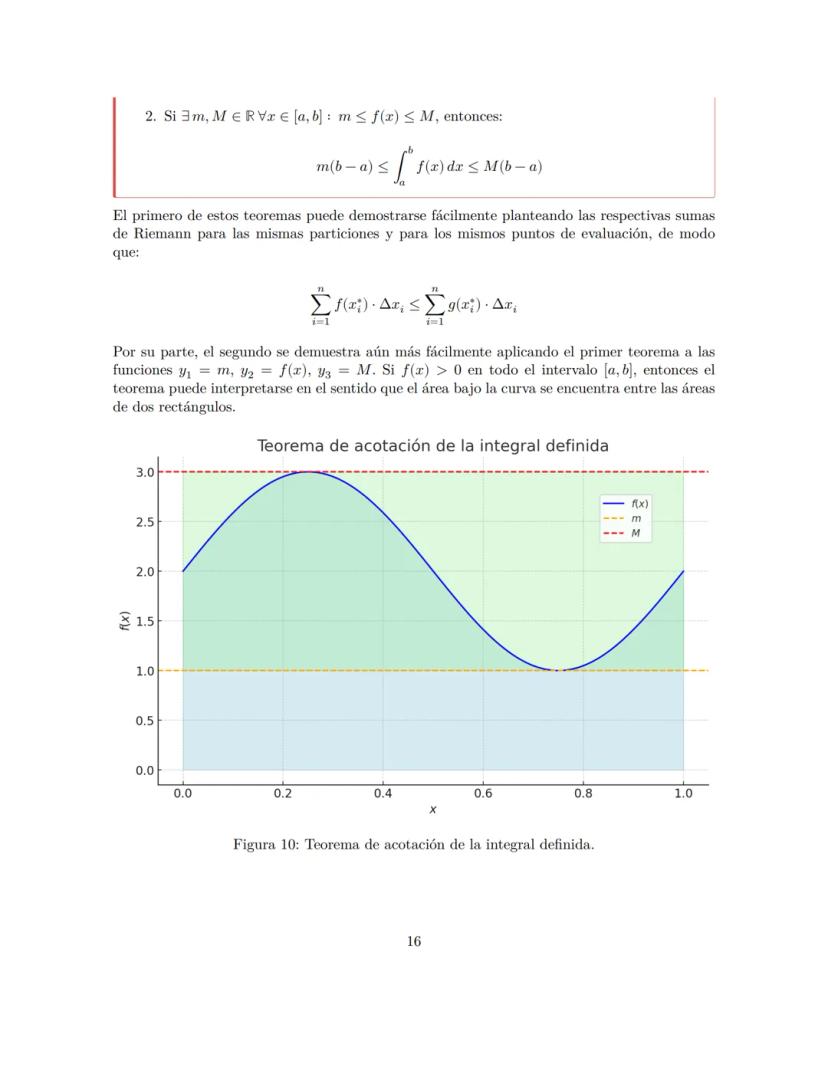
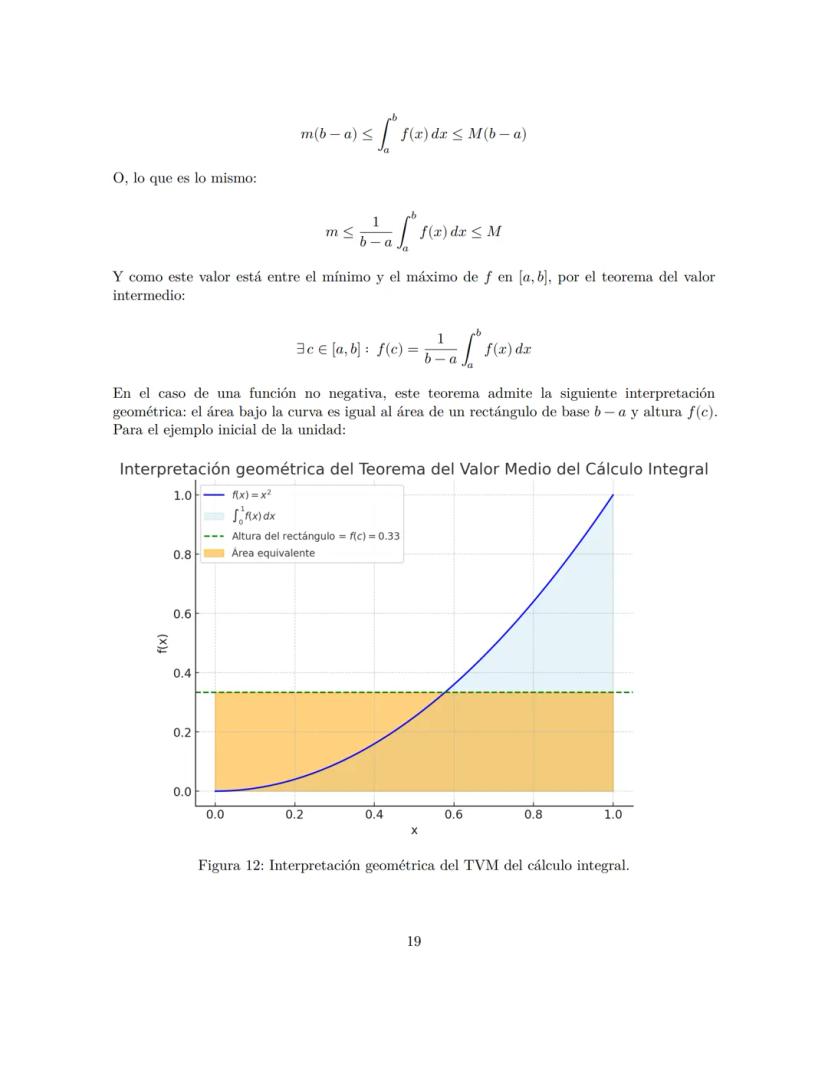
Una función inyectiva (o uno a uno) nunca repite valores en el rango. Si tenés dos valores diferentes de x, siempre van a dar valores diferentes de y. Para verificarlo, usá el criterio de la regla horizontal: si una línea horizontal toca la gráfica en más de un punto, no es inyectiva.
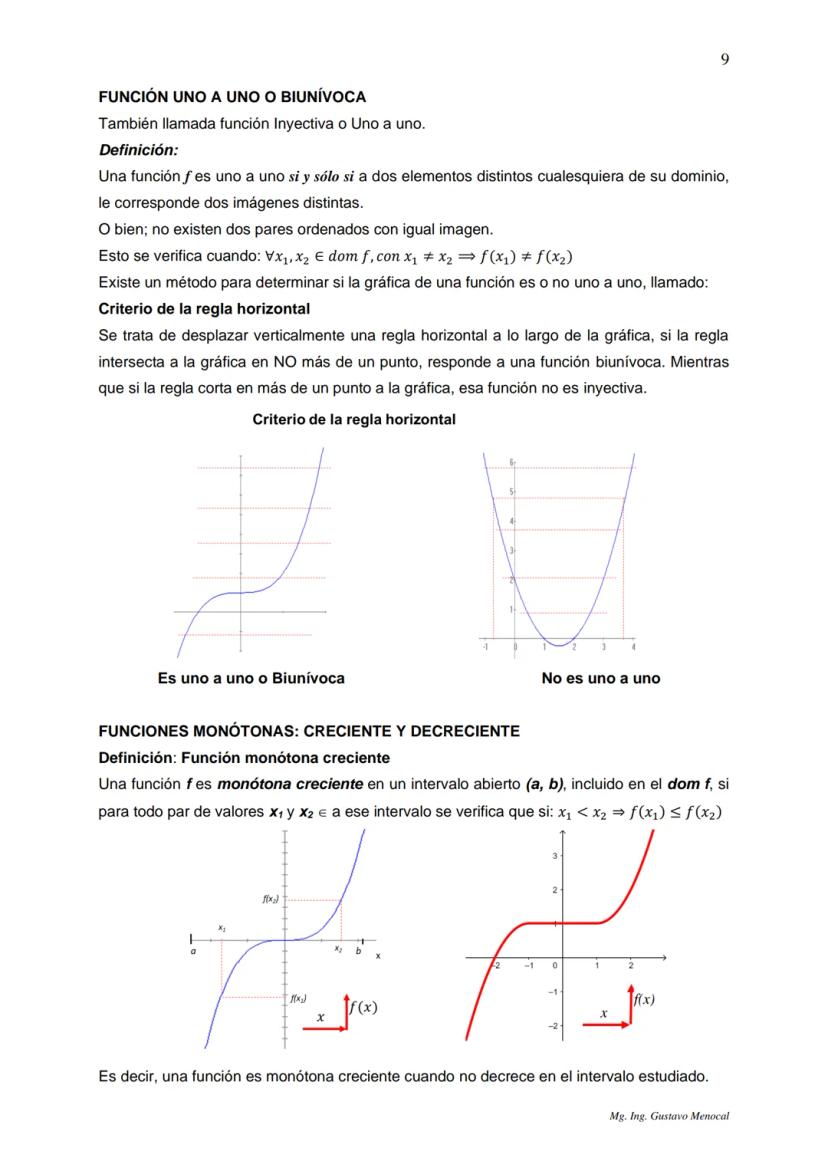
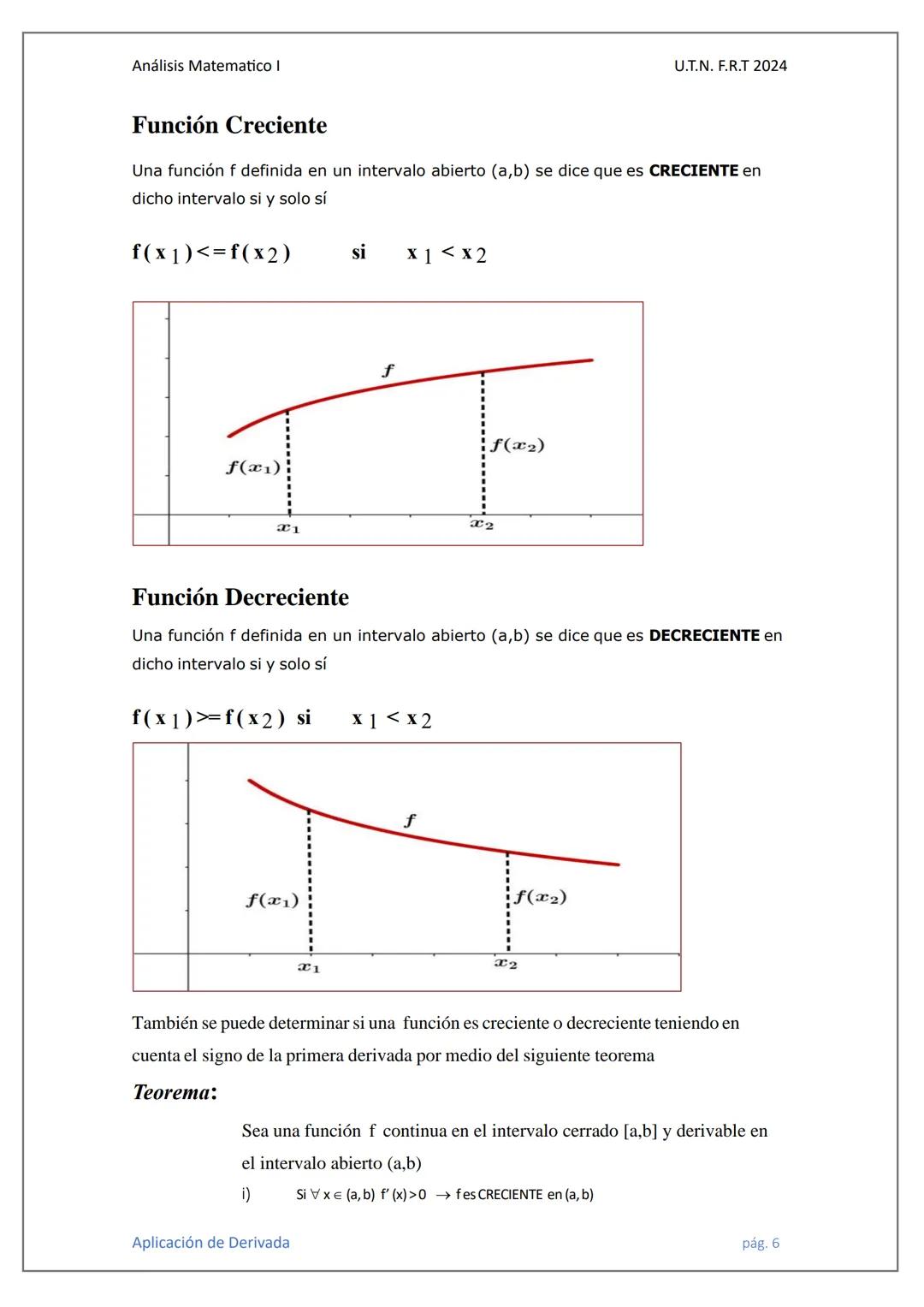
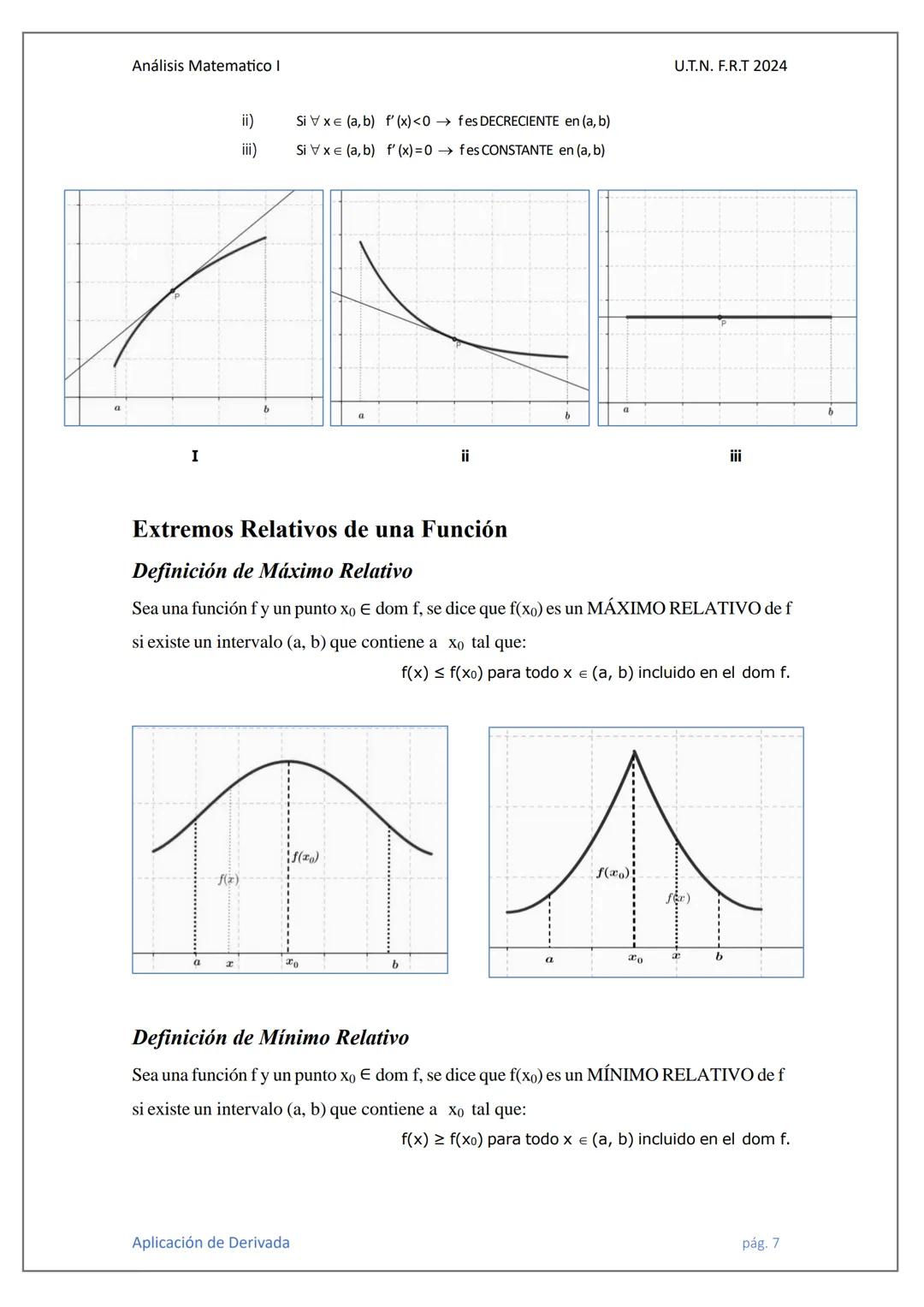
Las funciones monótonas crecientes nunca bajan. Si x₁ < x₂, entonces f(x₁) ≤ f(x₂). Pueden mantenerse iguales, pero jamás decrecer en el intervalo que estés analizando.
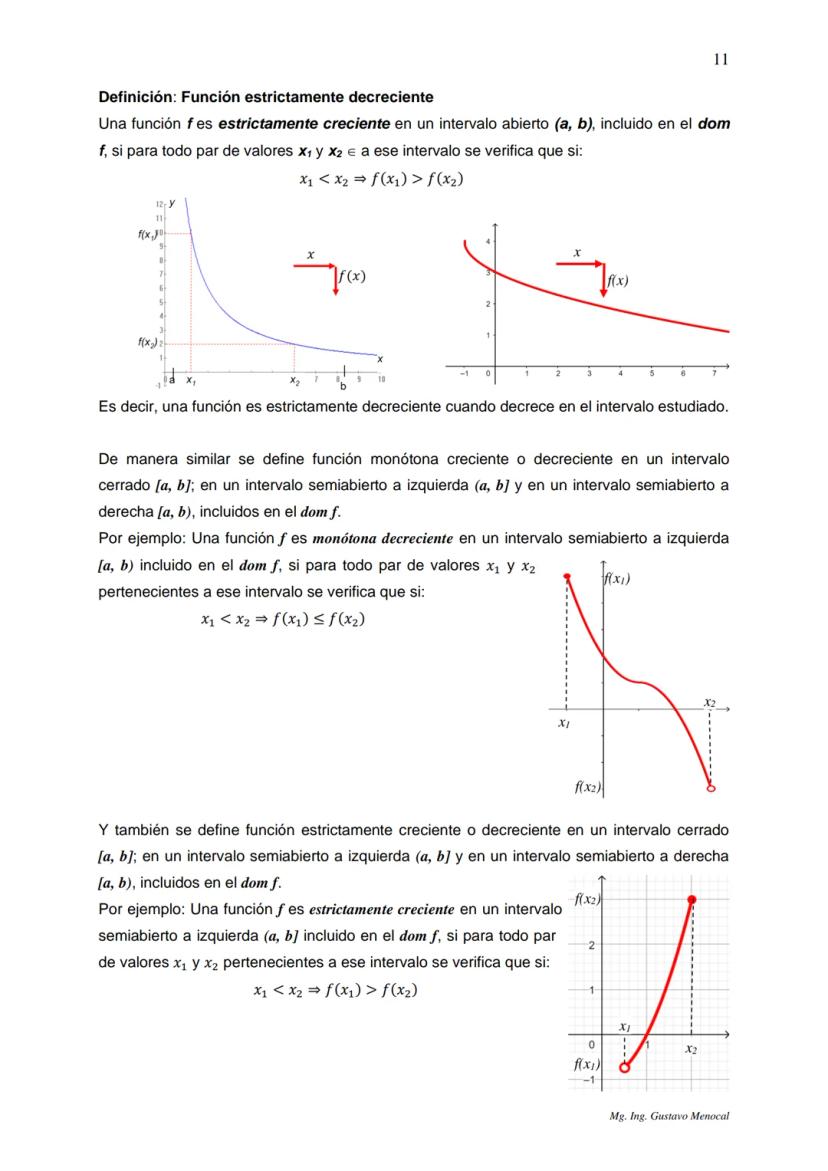
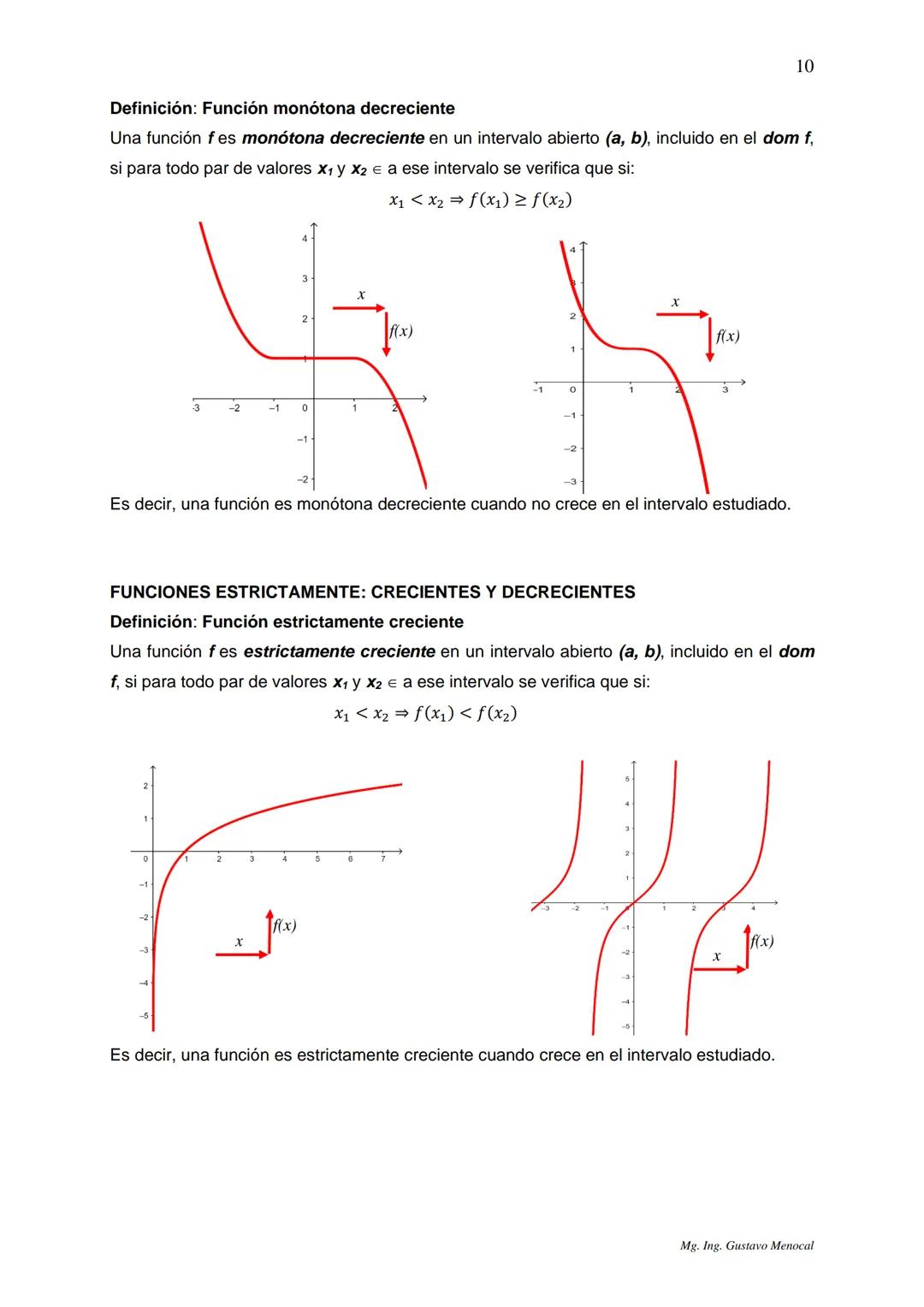
Las funciones monótonas decrecientes son lo opuesto: nunca suben. Si x₁ < x₂, entonces f(x₁) ≥ f(x₂). Pueden mantenerse constantes, pero no crecen.
Existe una versión más estricta: las funciones estrictamente crecientes siempre suben (f(x₁) < f(x₂)) y las estrictamente decrecientes siempre bajan. No se quedan constantes en ningún intervalo.
💡 Diferencia clave: "Monótona" permite tramos constantes, "estrictamente" no. ¡Es como la diferencia entre "no empeorar" y "mejorar siempre"!