Prefijos y Unidades en el Sistema Internacional

¿Alguna vez te preguntaste cómo se expresan cantidades muy grandes o muy pequeñas en Física? Los científicos usan prefijos que multiplican o dividen las unidades básicas.

Para denotar múltiplos o submúltiplos de unidades en el Sistema Internacional (SI), simplemente colocamos el símbolo del prefijo delante de la unidad. Cuando necesitamos aumentar el valor, multiplicamos $km = 1000 m$, y cuando queremos disminuirlo, dividimos $mm = 0,001 m$.

Los prefijos del SI nos permiten trabajar con magnitudes de cualquier tamaño de forma práctica. Por ejemplo, podemos pasar de kilómetros a metros, o de gramos a miligramos según necesitemos.

¡Dato clave! La notación científica expresa un número como el producto de un número entre 1 y 10 por una potencia de 10. Por ejemplo: 290 = 2,9 × 10² o 0,00015 = 1,54 × 10⁻⁴. Esto nos simplifica enormemente los cálculos con números muy grandes o muy pequeños.

Entre los prefijos más usados están:

• Múltiplos: kilo- (k, 10³), mega- (M, 10⁶), giga- (G, 10⁹)
• Submúltiplos: mili- (m, 10⁻³), micro- (μ, 10⁻⁶), nano- (n, 10⁻⁹)

Unidades de Magnitudes Físicas y Conversiones

En Física trabajamos con diferentes sistemas de unidades, pero el más utilizado es el Sistema Internacional (SI). Conocer las unidades de cada magnitud y cómo convertirlas es fundamental para resolver problemas correctamente.

Las magnitudes físicas más usadas tienen unidades específicas en cada sistema. Por ejemplo, la fuerza se mide en Newton (N) en el SI, en dinas en el sistema cegesimal, y en kilogramo-fuerza en el sistema técnico. La energía se mide en Joule (J) en el SI, en ergio en el sistema cegesimal, y en kilográmetro en el sistema técnico.

Para convertir unidades entre distintos sistemas existen dos métodos principales:

1. El factor de conversión: Multiplicamos el valor por una fracción donde el numerador y denominador son iguales pero expresados en unidades diferentes. Por ejemplo, para convertir 25 m/s a km/h:

25 m/s = 25 m/s · $1 km / 1000 m$ · $3600 s / 1 h$ = 90 km/h

2. Por sustitución: Reemplazamos cada unidad por su equivalente en el otro sistema. Para el mismo ejemplo:

25 m/s = 25 (10⁻³ km) / $1/3600 h$ = 90 km/h

¡Atención! Al trabajar con conversiones, asegúrate de que todas las unidades se cancelen correctamente, dejando solo las unidades que buscas en el resultado final.

Algunas conversiones comunes que debes recordar:

• 1 L = 0,001 m³ = 1000 cm³
• 1 h = 3600 s
• 0°C = 273 K
• 1 atm = 760 mmHg = 101300 Pa

Magnitudes Escalares y Vectoriales

En el mundo físico, las cantidades que medimos pueden ser de dos tipos principales: escalares y vectoriales. La diferencia es crucial para entender correctamente los fenómenos naturales.

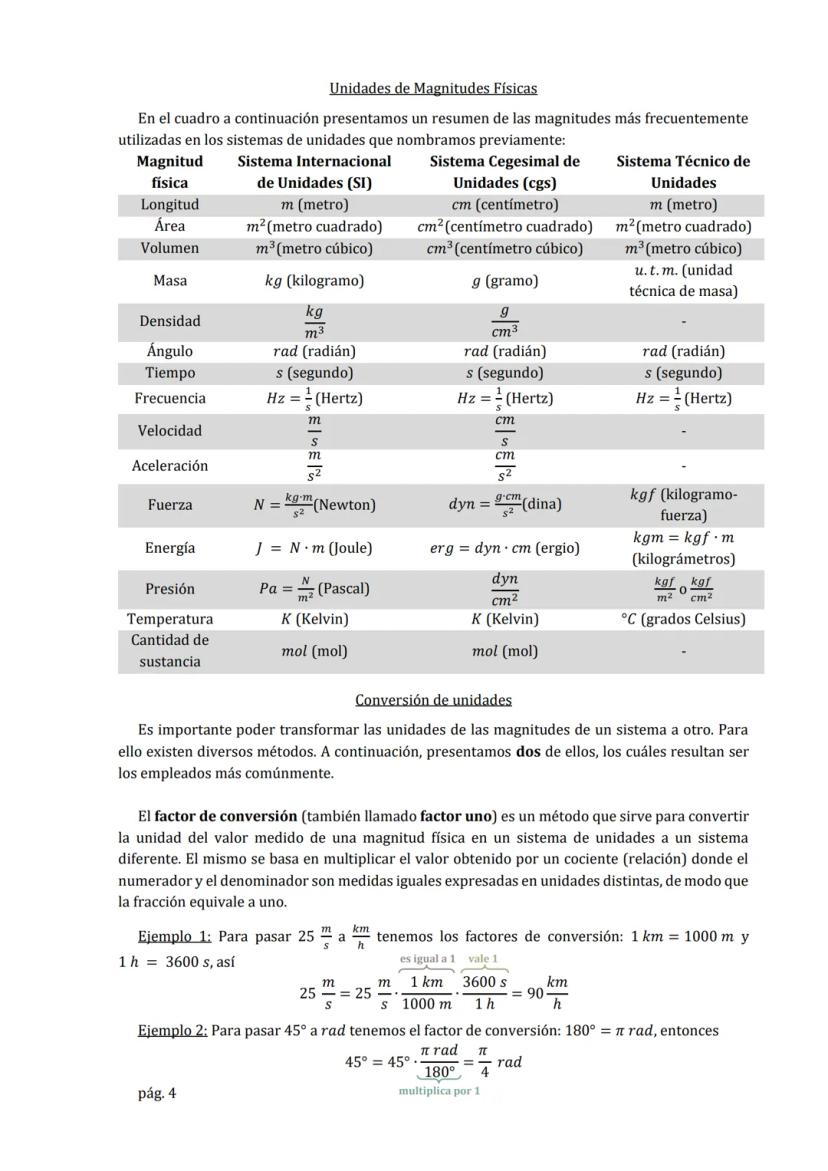
Las magnitudes escalares solo necesitan un valor numérico y su unidad para quedar completamente definidas. Por ejemplo, cuando dices que la temperatura es de 25°C o que el tiempo transcurrido fue de 10 segundos, estas cantidades quedan perfectamente determinadas con solo ese número y su unidad. Otros ejemplos son el volumen, la masa y la energía.

Por otro lado, las magnitudes vectoriales requieren algo más: además del valor numérico y la unidad, necesitan una dirección y un sentido. Por ejemplo, cuando describes una velocidad no basta con decir "60 km/h", también necesitas especificar hacia dónde se dirige (norte, este, hacia arriba, etc.). Otros ejemplos incluyen la aceleración, la fuerza, el peso y el campo eléctrico.

¿Por qué es importante esta distinción? Porque las magnitudes escalares y vectoriales se comportan de manera diferente cuando las combinamos. Por ejemplo, dos fuerzas (magnitudes vectoriales) de igual magnitud pero direcciones opuestas pueden cancelarse completamente, mientras que dos masas (magnitudes escalares) siempre se suman, independientemente de su posición.

Dato práctico: Las magnitudes vectoriales se representan con una flecha sobre el símbolo como $\vec{F}$ para la fuerza o en negrita (como v para la velocidad) para distinguirlas de las escalares.

Esta distinción será fundamental cuando estudiemos movimiento, fuerzas y otros conceptos físicos más avanzados.

Medición de Ángulos Planos

Los ángulos son fundamentales en Física, especialmente cuando estudiamos movimientos circulares, ondas o fuerzas en diferentes direcciones. ¿Cómo se miden correctamente?

Un ángulo plano se forma por dos semirrectas que comparten un punto de origen (vértice). Cuando medimos ángulos, podemos usar principalmente dos sistemas:

1. Sistema sexagesimal: Aquí la unidad es el grado (°), donde un ángulo completo (vuelta entera) mide 360°. Es el sistema que usamos con el transportador en geometría básica.

2. Sistema circular o radial: La unidad es el radián (rad). Un radián es el ángulo central de una circunferencia que subtiende un arco de longitud igual al radio. Este sistema es más natural para cálculos físicos y matemáticos.

La equivalencia entre ambos sistemas es: 360° = 2π rad

Esto significa que:

• 180° = π rad
• 90° = π/2 rad
• 60° = π/3 rad
• 45° = π/4 rad

¡Consejo! En Física, casi siempre trabajaremos con radianes en vez de grados, especialmente en ecuaciones de movimiento circular, ondas y oscilaciones. Los radianes hacen que las fórmulas sean más simples y elegantes.

Cuando un ángulo se mide en sentido antihorario se considera positivo, mientras que si gira en sentido horario será negativo. Esta convención es importante para describir correctamente rotaciones y movimientos circulares.

Geometría y Razones Trigonométricas

La geometría es esencial en Física para describir cómo están dispuestos los cuerpos y las fuerzas que actúan sobre ellos. Vamos a repasar algunos conceptos clave.

El Teorema de Pitágoras nos permite relacionar los lados de un triángulo rectángulo. Si tenemos un triángulo con catetos C₁ y C₂, e hipotenusa H, entonces:

H² = (C₁)² + (C₂)²

Este teorema es fundamental para calcular distancias y descomponer vectores en sus componentes.

Las razones trigonométricas nos ayudan a relacionar los ángulos y los lados de un triángulo rectángulo. Para un ángulo Â, definimos:

• Seno: sen  = cateto opuesto / hipotenusa
• Coseno: cos  = cateto adyacente / hipotenusa
• Tangente: tg  = cateto opuesto / cateto adyacente = sen  / cos Â

Estas relaciones son tremendamente útiles en Física para descomponer fuerzas, analizar movimientos en planos inclinados y resolver problemas de equilibrio.

Recordá que: La suma de los ángulos internos de cualquier triángulo siempre es 180°. Esto te puede ayudar a encontrar ángulos desconocidos cuando tengas dos de ellos.

Cuando trabajamos con triángulos rectángulos (que tienen un ángulo de 90°), las razones trigonométricas son herramientas poderosas que nos permiten encontrar longitudes y ángulos desconocidos. ¡Dominarlas te facilitará enormemente la resolución de problemas físicos!

Perímetros y Áreas de Figuras Planas

En Física frecuentemente necesitamos calcular áreas y perímetros para resolver problemas de presión, trabajo, flujo de calor o momentos de inercia. Tener estas fórmulas a mano nos ahorrará tiempo.

Para las figuras más comunes, recordemos:

Cuadrado (lado l):

• Perímetro: P = 4l
• Área: A = l²

Rectángulo (lados a y b):

• Perímetro: P = 2$a + b$
• Área: A = a·b

Triángulo (base a, altura h, lados a, b y c):

• Perímetro: P = a + b + c
• Área: A = (a·h)/2

Trapecio regular (bases paralelas a y c, altura h):

• Perímetro: P = a + 2b + c
• Área: A = $(a + c)/2$·h

Consejo práctico: Cuando trabajés con áreas irregulares, podés dividir la figura en formas geométricas básicas (triángulos, rectángulos, etc.) y sumar sus áreas individuales.

Recuerda que el romboide (paralelogramo) con lados a y b, y altura h tiene un área A = a·h, mientras que el trapezoide (cuadrilátero sin lados paralelos) puede descomponerse en triángulos para calcular su área.

Estas fórmulas no son solo para memorizar, sino para entender cómo se relacionan las dimensiones con el área y el perímetro. Esta comprensión es fundamental cuando analices problemas físicos que involucren superficies y distancias.

Áreas de Polígonos Regulares y Circunferencias

Los polígonos regulares y las circunferencias aparecen frecuentemente en problemas de física, desde el movimiento circular hasta campos electromagnéticos. ¡Dominemos sus propiedades!

Para los polígonos regulares (todos los lados y ángulos iguales), el área se puede calcular usando la apotema (ap), que es la distancia perpendicular del centro a cualquier lado:

• Pentágono regular (5 lados):

  • Perímetro: P = 5·l
  • Área: A = (5·l·ap)/2

• Hexágono regular (6 lados):

  • Perímetro: P = 6·l
  • Área: A = (6·l·ap)/2

• Heptágono regular (7 lados):

  • Perímetro: P = 7·l
  • Área: A = (7·l·ap)/2

• Octágono regular (8 lados):

  • Perímetro: P = 8·l
  • Área: A = (8·l·ap)/2

Para la circunferencia (radio r, diámetro d):

• Perímetro (longitud): P = 2π·r = π·d
• Área: A = π·r² = (π·d²)/4

Dato curioso: ¿Sabías que para cualquier polígono regular de n lados, el área se puede calcular como A = (n·l·ap)/2? Esta fórmula general te permite trabajar con cualquier polígono regular.

El conocimiento de estas fórmulas es particularmente útil cuando estudiamos rotaciones, momentos de inercia y distribuciones circulares, situaciones muy comunes en física tanto teórica como aplicada.

Volúmenes de Cuerpos Geométricos

El cálculo de volúmenes es esencial en física para determinar densidades, presiones hidrostáticas, y analizar fuerzas de flotación, entre otras aplicaciones. Estas fórmulas te serán muy útiles.

Cubo (lado l):

• Volumen: V = l³

Prisma rectangular (lados a, b y c):

• Volumen: V = a·b·c

Cilindro (radio r, altura h):

• Volumen: V = π·r²·h
• También: V = (π/4)·d²·h $con d = diámetro$

Esfera (radio r, diámetro d):

• Volumen: V = (4/3)π·r³
• También: V = (π/6)·d³

Pirámide de base cuadrada (lado de base l, altura h):

• Volumen: V = (l²·h)/3

Tetraedro regular (arista a):

• Volumen: V = (√2/12)·a³

Concepto clave: Para muchos cuerpos geométricos, el volumen se puede calcular como el producto del área de la base por la altura, dividido por un factor que depende de la forma. Por ejemplo: pirámides y conos (factor 3), mientras que prismas y cilindros (factor 1).

Estas fórmulas son especialmente importantes cuando trabajás con fluidos, gases o cuando analizás la distribución de masa en diferentes cuerpos. El dominio de estos conceptos te permitirá resolver problemas de física más complejos con mayor facilidad.

Rectas Paralelas y Geometría Analítica

La geometría no es solo una herramienta matemática, sino una forma de visualizar y resolver problemas físicos. Entendamos dos conceptos clave: las rectas paralelas y la geometría analítica.

Cuando dos rectas paralelas son cortadas por una tercera (secante), se forman ocho ángulos con propiedades específicas que nos ayudan a resolver muchos problemas de física:

• Ángulos alternos internos: son iguales entre sí
• Ángulos alternos externos: son iguales entre sí
• Ángulos correspondientes: son iguales entre sí
• Ángulos opuestos por el vértice: son iguales (esto siempre es cierto)
• Ángulos adyacentes: son suplementarios (suman 180°)

Estas propiedades son fundamentales para analizar fuerzas en equilibrio, vectores en el plano y muchas otras situaciones físicas.

La geometría analítica, desarrollada por René Descartes, nos permite representar el espacio mediante coordenadas. Vivimos en un espacio tridimensional, lo que significa que necesitamos tres coordenadas para ubicar un punto. El sistema de referencia cartesiano ortogonal utiliza tres ejes perpendiculares entre sí (x, y, z).

¡Idea importante! Aunque nuestro mundo es tridimensional, muchos problemas de física pueden simplificarse a una o dos dimensiones. Por ejemplo, el movimiento de un proyectil puede analizarse en un plano (bidimensional), y el movimiento de un objeto en caída libre puede estudiarse en una línea (unidimensional).

En este sistema, un punto Q se representa por sus tres coordenadas: Q(x₀, y₀, z₀). Esta forma de representar el espacio es la base para entender vectores y campos, conceptos esenciales en la física moderna.

Vectores: Conceptos Básicos

Los vectores son herramientas matemáticas fundamentales en física para representar magnitudes que tienen dirección, como velocidad, fuerza o campo eléctrico. ¿Cómo se definen y utilizan?

Un vector es un segmento orientado determinado por dos puntos: un origen (O) y un extremo (E). Gráficamente se representa con una flecha que indica el sentido. Todo vector tiene tres características esenciales:

• Módulo: la longitud del segmento (cuánto)
• Dirección: la recta que contiene al vector (por dónde)
• Sentido: la orientación dentro de esa recta (hacia dónde)

Para trabajar en espacios de diferentes dimensiones, usamos sistemas de referencia:

• En una dimensión (recta): necesitamos un eje (generalmente "x")
• En dos dimensiones (plano): necesitamos dos ejes perpendiculares ("x" e "y")
• En tres dimensiones (espacio): necesitamos tres ejes perpendiculares ("x", "y" y "z")

Ejemplo práctico: Cuando describimos la velocidad de un auto, no basta con decir "100 km/h" (magnitud escalar). Necesitamos especificar también hacia dónde se dirige, como "100 km/h hacia el este" (magnitud vectorial).

Un concepto importante es el vector nulo (0), que tiene módulo cero y carece de dirección y sentido. También existe el versor o vector unitario, que tiene módulo uno y se usa para indicar direcciones. El vector opuesto $-a$ tiene el mismo módulo y dirección que el original, pero sentido contrario.

Estos conceptos son la base para entender cómo las fuerzas, velocidades y otras magnitudes físicas interactúan en el mundo real.